因为课题的需要,需要把之前代码里的ceres计算里程计重构成基于gtsam计算里程计,这篇博客做个总结,主要是针对FLOAM和ALOAM这两套代吗的重构,ALOAM重构没出什么问题,但是FLOAM重构出现了比较严重的问题,下面会详细描述.
Introduction
首先明确一点, ceres, g2o, gtsam本质上都是可以用来求解非线性最小二乘问题的, 所以, 里程计模块用gtsam是可行的。
出发点: 将前端里程计的因子都在gtsam中构建,方便建立全局因子图进行优化,另外根据相关文献[1]结果:
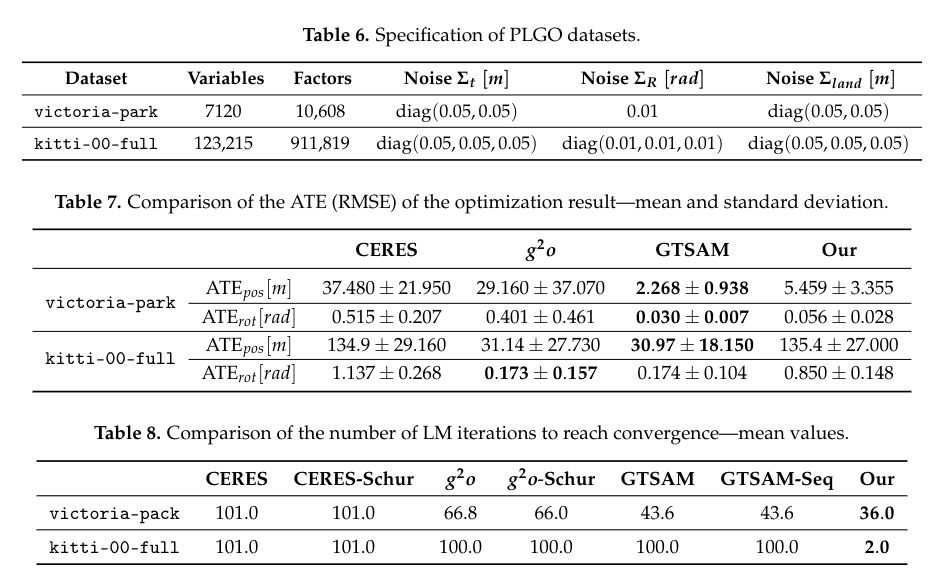
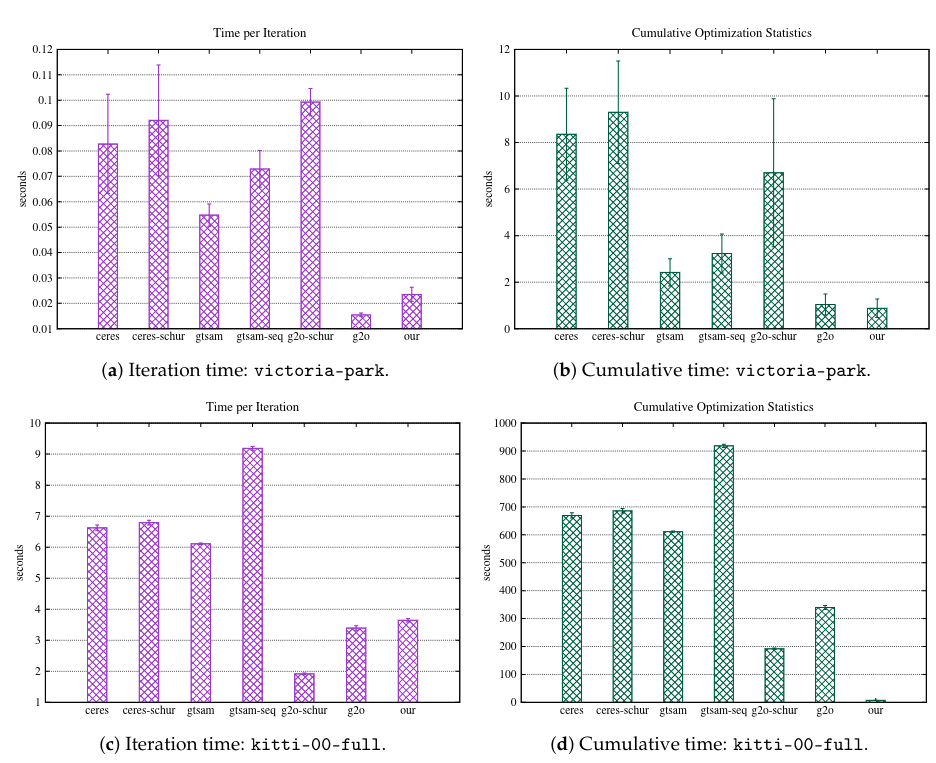
精度比较&时间比较:
gtsam>g2o>ceres(accuracy); g2o>ceres>gtsam(time)
也就是说gtsam优化出的精度是比较高的,但是时间是比较长的.
具体是不是这样呢?后面会通过自己设计的实验进行对比.
参考gtsam_examples, gtsam自定义一个因子大体分为两步:
- 自定义残差
- 自定义雅可比
(是不是和ceres很像?hhh)
下面分别用Aloam改gtsam和Floam改gtsam的例子来说明.
ALOAM converted to gtsam
写完了才发现已经有人做过类似的工作, 当然我自己的代码也完成了,博客整理完毕后也会进行发布, 各位看官莫急。
首先回顾下ALOAM的残差和雅可比计算:
- 残差
-
点线残差:
lp = q_last_curr * cp + t_last_curr;
Eigen::Matrix<T, 3, 1> nu = (lp - lpa).cross(lp - lpb); Eigen::Matrix<T, 3, 1> de = lpa - lpb;
residual[0] = nu.x() / de.norm(); residual[1] = nu.y() / de.norm(); residual[2] = nu.z() / de.norm();
-
点面残差:
Eigen::Matrix<T, 3, 1> ljm{T(ljm_norm.x()), T(ljm_norm.y()), T(ljm_norm.z())};= Eigen::Matrix<T, 3, 1> lpj{T(last_point_j.x()), T(last_point_j.y()), T(last_point_j.z())}; residual[0] = (lp - lpj).dot(ljm);
-
- 雅可比
Aloam用的是解析求导,没有手写雅可比.
转换成gtsam
首先残差肯定是不变的,那么需要额外补充的就是雅可比的计算,先是推导出这两个雅可比的数学形式(注意,gtsam所优化的pose3已经是个se3, 所以不需要过参数化,前三维旋转,后三维平移):
激光角点残差及其雅可比推导
\[errror=\frac{(lp-lpa)\times(lp-lpb)}{(||lpa-lpb||)}\\ constant\ value:\ lpa,lpb,lpa-lpb\\ set:\ Jacobin=\frac{d(error)}{dT}=\frac{1}{||lpa-lpb||}*(\frac{d(lp-lpa)}{dT}\times(lp-lpb)+(lp-lpa)\times\frac{d(lp-lpb)}{dT})\\ =\frac{1}{||lpa-lpb||}*((lpb-lpa)\times\frac{dlp}{dT})\\ =\frac{1}{||lpa-lpb||}*((lpb-lpa){^{\wedge }}\cdot\frac{dlp}{dT})\\ \frac{dlp}{dT}=[P^{\wedge}|I]\]激光面点残差及其雅可比推导
\[error=(lp-lpj)\cdot{\frac{(lpj-lpl)\times(lpj-lpm)}{\|(lpj-lpl)\times(lpj-lpm)\|}}\\ =(lp-lpj)\cdot ljk\\ Jacobian = \frac{d((lp-lpj)\cdot ljk)}{dlp}\cdot\frac{dlp}{dT}(这两个gtsam可以直接算)\\ 或者继续手推:=\frac{d(lp\cdot ljk)}{dT}\\ =ljk^T\cdot\frac{dlp}{dT}\\ \frac{dlp}{dT}=[P^{\wedge}|I]\]FLOAM converted to gtsam
与上面类似,但是需要注意残差形式有点变化,FLOAM的面残差直接走的法向量。
时间对比(ALOAM)
Seq 04: 114ms vs 97ms
…..
To be done
精度对比(ALOAM)
(Rmse) Seq 04 : 2.11 vs 2.87
…..
To be done
