本篇论文解读已投稿至3D视觉工坊,记录在个人博客仅供个人学习记录,商业转载行为请联系3D视觉工坊公众号
《TwistSLAM: Constrained SLAM in Dynamic Environment》(RAL 2022)
111## Motivation
现有的视觉SLAM一般假定环境是刚性的,这种假设很大程度上限制了算法的应用,因为现实环境是动态变化的(汽车,行人等)。现有的解决方法一是通过动态物体去除来缓解这个问题,但是随着动态物体点占比的提升,直接采取去除的方式会大大降低定位的精度;二是利用深度学习来标注动态物体从而来维持静态环境的假设,但是这样会导致环境信息的丢失;三是基于语义来同时解决SLAM和目标跟踪问题,这也是这篇文章的技术基础之一。
下图是算法的示意图: 算法同时估计相机位姿和场景中的移动对象,场景中的地图结构(图中为道路平面)会约束对象的移动。算法框架基于的是ORB-SLAM2,在建图时,会同时使用语义信息来构建与场景中对象对应的簇地图,簇地图构建完成后,可以仅利用静态簇(道路和房屋)来估计位姿。动态簇可以通过速度的变化来进行跟踪和约束。
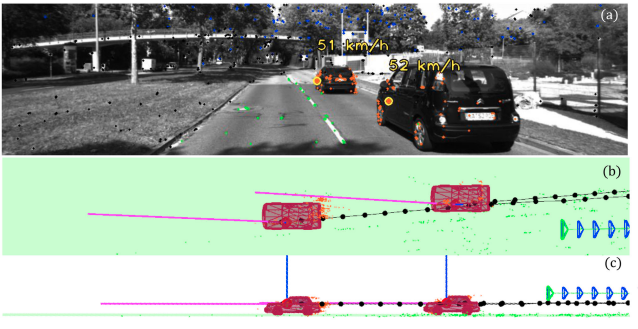
另外,目前虽然也有可以跟踪动态物体的SLAM,但是他们绝大部分都是使用重投影误差之类的优化项,这些都是6个自由度。这其实与现实世界并不符合,比如说,大部分汽车只有3个自由度,2个自由度在平移(道路平面),1个自由度在旋转(汽车自身法向量)。所以消除与物理意义不对应的自由度也是有必要的。对应这个问题的解决办法,作者是选择将约束表示为机械关节,因为机械关节的运动是有限制的,从而减少了自由度。
Contribution
- 提出了一种语义SLAM系统,可以在静态和动态场景中可靠地估计相机的位姿。
- 提出了一个可以跟踪场景中多个移动对象的立体SLAM框架。
- 提出了一种新的跟踪和BA公式,该公式考虑了场景中对象之间的机械关节特性,从而约束运动的自由度。
Content
- 符号声明
刚性物体o关于世界坐标系的位姿:
\[{ }^{w} \mathbf{T}_{o_{i}}=\left(\begin{array}{cc} { }^{w} \mathbf{R}_{o_{i}} & { }^{w} \mathbf{t}_{o_{i}} \\ 0 & 1 \end{array}\right) \in \text{SE}(3)\]运动物体的速度可以表示为一个twist:
\[\boldsymbol{\xi}=\left(\begin{array}{llllll} v_{x} & v_{y} & v_{z} & \omega_{x} & \omega_{y} & \omega_{z} \end{array}\right)^{\top}=\left(\begin{array}{ll} \mathbf{v} & \boldsymbol{\omega} \end{array}\right)^{\top} \in \mathbb{R}^{6}\]twist同时也可以表示为矩阵:
\[[\boldsymbol{\xi}]_{\wedge}=\left(\begin{array}{cc} {[\boldsymbol{\omega}]_{\times}} & \mathbf{v} \\ 0 & 0 \end{array}\right) \in \text{se}(3)\]关于twist的指数映射:
\[[\boldsymbol{\xi} \delta t]_{\wedge} \in \text{se}(3) \longrightarrow \mathbf{T} \in \text{SE}(3)\]那么运动物体在桢间的运动可以表示为:
\[{ }^{w} \mathbf{T}_{o_{i+1}}=\exp \left({ }^{w} \boldsymbol{\xi}_{o_{i}} \delta t_{i}\right)^{w} \mathbf{T}_{o_{i}}={ }^{w} \mathbf{T}_{o_{i}} \exp \left({ }^{o_{i}} \boldsymbol{\xi}_{o_{i}} \delta t_{i}\right)\]同一个物体同一时间在不同坐标系的表示可以通过伴随映射矩阵来转换:
\[{ }^{w} \boldsymbol{\xi}_{o_{i}}={ }^{w} \mathbf{V}_{o_{i}}{ }^{o_{i}} \boldsymbol{\xi}_{o_{i}}\]伴随映射矩阵可以通过不同坐标系的相对位姿来构建:
\[^wV_{o_i}=\begin{pmatrix} ^wR_{o_i} & [^wt_{o_i}]_\times ^wR_{o_i}\\ 0 & ^wR_{o_i} \end{pmatrix}\]-
语义簇图
语义簇图是作者提出的一个数据结构,图的顶点对应于场景中的对象,边对应于对象之间存在的物理链接, 示意图如下:
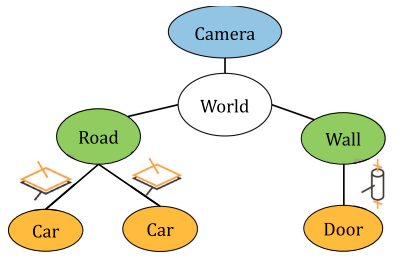
目标是估计相机的位姿和每个移动对象的位姿,同时使用对象之间的机械关节来改进这些位姿估计,上图的两个汽车簇都通过一个平面约束链接到道路,该约束仅具有3自由度(1个关于平面法向量的旋转自由度,2个平面内的平移自由度)。 这样的简单表示允许具有高度通用性,因为对于给定的语义类,只需要定义其静态父类和优化的机械关节的类型。
- 算法框图
如下图。使用语义信息创建与场景中的对象相对应的点簇。然后使用静态语义簇(例如道路、地板、房子)来鲁棒地跟踪相机。接下来,匹配与动态对象(例如,汽车、自行车等)对应的关键点,通过双目图片跟踪或三角化新的3D点。然后,在BA中,使用静态和动态3D点对相机和对象的所有位姿估计进行优化
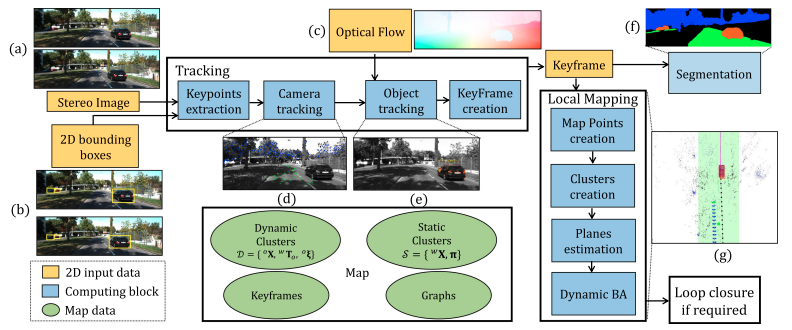
-
从全景分割创建簇
这一步,作者选择基于S3LAM的全景分割方式来创建簇。全景图像的优点在于能够知道图像中每个像素的语义类,并为每个对象指定唯一的id。然后融合单个3D点的多个2D观测值,以获得其类别和id,从而获得最终的语义地图。因为静态对象是固定的,所以在直接表示他们的三维点;对于动态对象,通过簇位姿和簇twist来表示。
-
簇几何
这一部分的目标是为计算机械关节约束动态簇的速度和位姿作铺垫。假设仅考虑平面簇,对于每一个平面簇都可以通过SVD估计出一个三维平面,然后通过RANSAC去除离群值。
- 动态SLAM
首先是仅使用静态点簇的点来计算相机位姿,代价函数如下:
\[E\left({ }^{c_{i}} \mathbf{T}_{w}\right)=\sum_{j \in \mathcal{S}} \rho\left(\left\|{ }^{i} \mathbf{x}_{j}-p\left({ }^{c_{i}} \mathbf{T}_{w},{ }^{w} \mathbf{X}_{j}\right)\right\|_{\Sigma_{i, j}^{-1}}\right)\\ p是针孔相机投影,{\Sigma_{i, j}^{-1}}是重投影误差的协方差\]考虑到如果场景中包含许多实际上是静态的潜在移动对象,例如停放的汽车,则位姿可能会变差。为了解决这个问题,可以估计所有运动对象的位姿,并将它们集成到BA中,将速度接近0的动态对象点也作为静态点。
- 动态数据关联和关键点
动态数据关联的挑战主要有两个,一个是相机和对象运动的组合会在图像空间中产生较大的位移,因此需要进行大半径搜索以匹配关键点,另一个是较大的移动可能会导致图像中对象的重要视觉变化(例如,对象的亮度变化或视点变化),这使得匹配过程更加困难。
作者采用的是RAFT中所用的CNN产生光流估计的方法来解决上述问题。
目标跟踪的问题是动态对象通常占据图像的一小部分,导致目标点太少,无法获得精确的估计。
对于这个问题,作者强制关键点提取过程从对象边界框定义的区域中保留更多的关键点。然后使用关键点创建具有双目三角剖分的新三维点,并且将这些点添加到现有簇中或用于创建新簇,或者直接用来进行跟踪。
- 簇间约束的机械关节
首先提出一个假设:大部分移动簇可以通过特定的机械关节链接到静态父簇。根据ISO3952,存在有12个标准关节。作者主要使用的是平面关节(3个自由度:平面中的2个平移和围绕其法线的1个旋转,表示汽车相对于其静态父对象道路的位移)和旋转关节(1自由度。静态父簇是墙,移动簇是门)。
为了更方便的建模关节,可以将twist的空间分解为两个正交空间的和:
\[\mathbb{R}^{6}=\mathbb{F}_{l}+\mathbb{F}_{l}^{\top}\]Fl表示通过关节l约束的twist的空间在坐标系F下的表示。对于具有z轴的平面关节,Fl定义为:
\[\mathbb{F}_{l}=\text{Span}\left(\left(\begin{array}{llllll} 1 & 1 & 0 & 0 & 0 & 1 \end{array}\right)^{\top}\right)\]要使对象的位移在物理上精确,twist必须位于Fl空间内。为此,将twist从其原始空间投影到Fl。因为R6是欧几里德矩阵,所以投影是一个6×6矩阵,定义如下:
\[\mathbb{F}_{l}=\text{Span}\left(\mathbf{A}_{l}\right) \\ \Pi_{l}=\mathbf{A}_{l}\left(\mathbf{A}_{l}^{\top} \mathbf{A}_{l}\right)^{-1} \mathbf{A}_{l}^{\top}\]举个例子,如果是平面关节,那么:
\[\Pi_{l}=\left(\begin{array}{llllll} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \end{array}\right)\]那么,twist关于这个平面关节的变换可以表示为:
\[\boldsymbol{\Pi}_{l} \boldsymbol{\xi}=\left(\begin{array}{llllll} v_{x} & v_{y} & 0 & 0 & 0 & \omega_{z} \end{array}\right)^{\top}\]注意,这时候,关于twist的自由度也就只有3个了,通过这个约束,可以修改重投影方程:
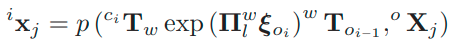
上述重投影方程只在关节坐标系成立,如果要到世界坐标系,那么就加上伴随投影,所以最终的世界坐标系的3自由度重投影方程定义为:
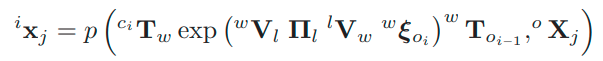
通过上述的重投影方程,可以构建出与动态对象点对应的twist的优化项:
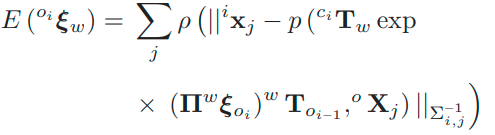
然后帧中的动态对象点位姿可以更新为
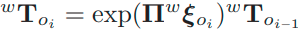
- 动态BA
动态BA有多个目标。首先,优化动态对象的位姿及其三维点的位置。其次,它允许链接对象和相机位姿,实际上,如果BA没有考虑动态对象,只有相机位姿对对象位姿产生影响,会导致性能的下降。考虑随时间估计位置的动态点,可以使用它们来优化相机位姿,但由于对象的位姿估计更具噪声,因此精度较低。最后,对twist应用软约束,从而获得更平滑的轨迹和速度。整体的BA代价函数定义如下:
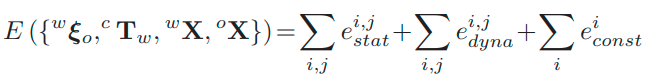
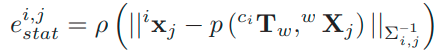
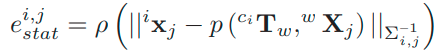
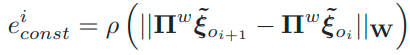
- BA的雅克比
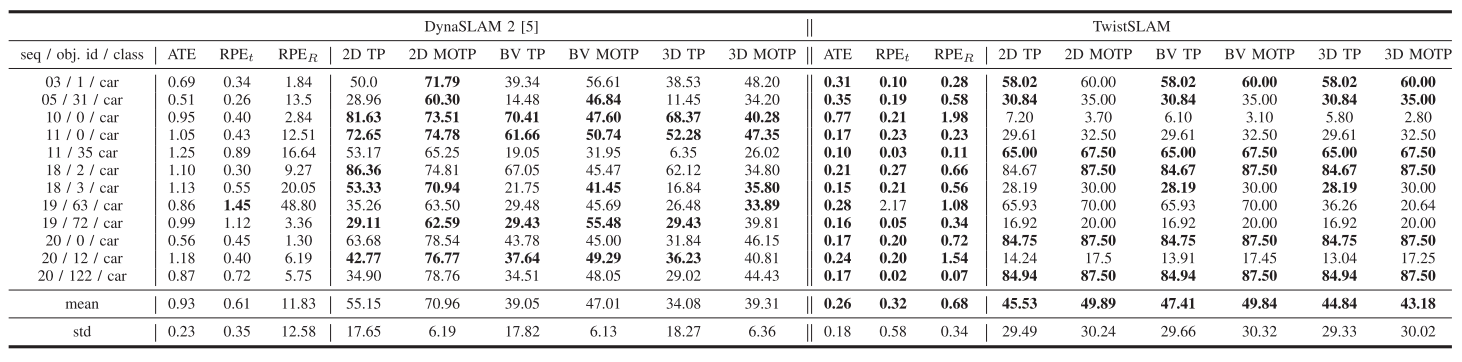
- 实验结果
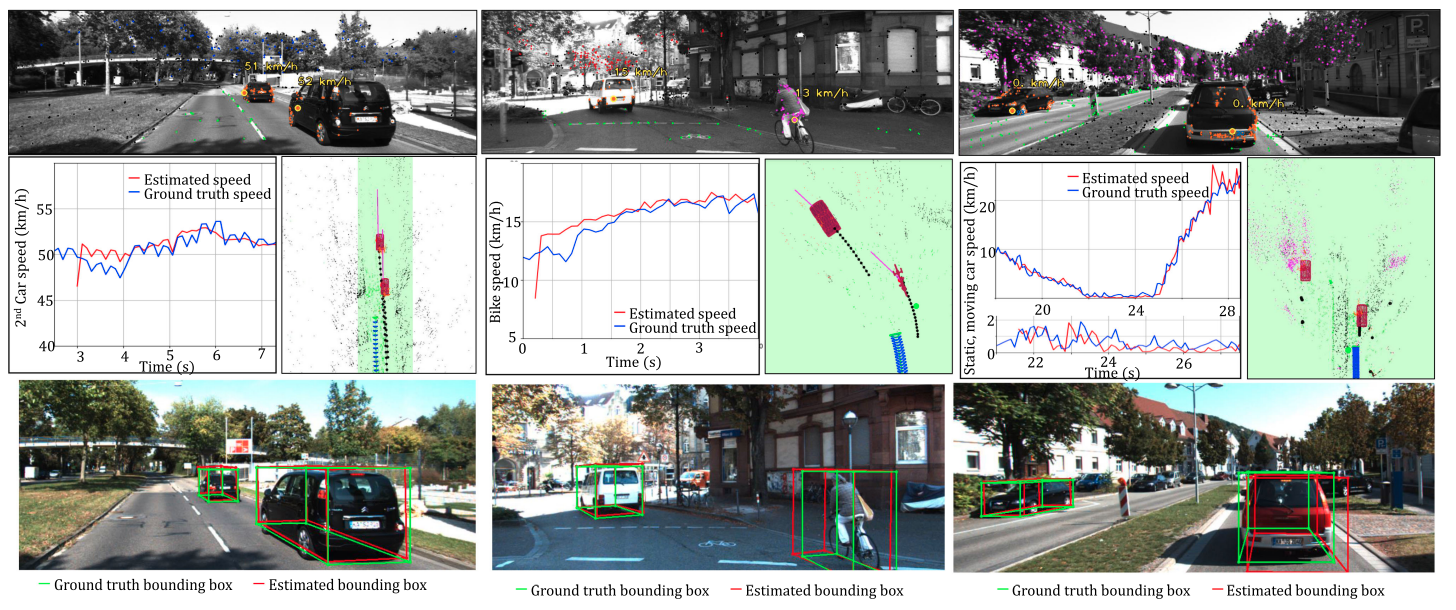
实验均在KITTI数据集上完成,就相机位姿估计和目标位姿估计两个指标来看,都实现了sota的精度。
Conclusion
作者提出了一种新的双目语义动态SLAM系统,既可以估计摄像机的姿态,也可以跟踪场景中的所有动态对象。使用簇之间的机械关节,可以将对象运动约束为物理上可能的运动,这可以改进相机和对象的位姿估计,因为更符合物理意义,同时也可以减少运算量。
