GPU加速，本质上还是LI-SLAM,里程计基于关键帧进行固定滞后平滑优化，然后在全局建图模块再一次进行因子图的优化。时间上通过GPU加速体素格GICP因子和IMU预积分因子的计算以及融合。

本篇论文解读已投稿至3D视觉工坊，记录在个人博客仅供个人学习记录，商业转载行为请联系3D视觉工坊公众号

《Globally Consistent and Tightly Coupled 3D LiDAR Inertial Mapping》(ICRA 2022)

Motivation

Lidar和IMU的结合是比较重要的，并且目前发展的也相对比较成熟。但是问题在于，目前Lidar和IMU的紧耦合主要集中在前端里程计，基本没有涉及到后端全局优化以及建图的融合。作者认为是因为后段全局优化通常采用的是图优化，并且图优化的先验位姿通常是前端的相对位姿，所以导致了后端优化的时候通常IMU和LIDAR是分离的，通常只优化LIDAR。所以作者就想到设计一个在所有阶段(前端里程计+后端全局优化和建图)，IMU和LIDAR都紧耦合的SLAM系统。

Contribution

1. 文章使用的是基于体素化的 GICP 匹配成本因子，与常用的基于线和平面点匹配的扫描匹配相比，它使用更多的点来计算配准误差。这可以在充分利用 GPU 并行处理的同时实现对传感器姿态的准确和稳健的约束。
2. 紧密耦合的里程计估计模块采用基于关键帧的固定滞后平滑方法，该方法可以实现具有有限计算成本的低漂移轨迹估计。
3. 后端同样采用了紧密耦合的方法。后端在 IMU 因子的支持下构建了一个密集连接的匹配成本因子图，并表现出出色的准确性。它还引入了子图端点的概念，以在具有 IMU 约束的大时间间隔内强约束子图。

Content

1. 系统框架

   系统框架如下图，主要包括4个模块，预处理模块，前端里程计模块，局部建图模块，全局建图模块，所有模块都是LIDAR-IMU紧耦合的。里程计模块提供一个初始位姿，然后通过局部建图模块进一步细化，最后将多个局部地图合并成子图送入全局建图模块中优化。所有的这些模块都是通过多线程并行运行。

   

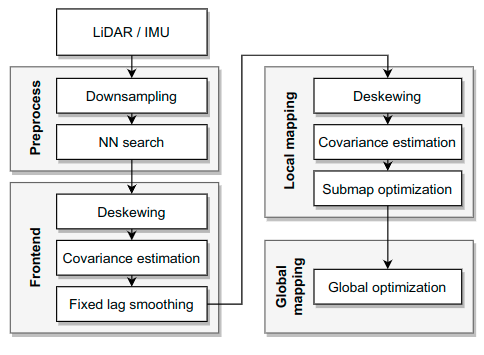
2. LIDAR匹配残差因子

   文章里选用的是GICP(VGICP)代价函数，因为它是适用于GPU加速的。VGICP 将每个输入点 $p_k\in P_i$ 建模为高斯分布 $p_k = (\mu_k,C_k)$，协方差矩阵 $C_k$ 由 $p_k$ 的相邻点计算得出。初始点云首先是被体素格化，然后再进行计算高斯分布以及协方差。基于GICP的两个点云之间的代价函数可以表示为：

\[\begin{aligned} e^{M}\left(\mathcal{P}_{i}, \mathcal{P}_{j}, \boldsymbol{T}_{i}, \boldsymbol{T}_{j}\right) &=\sum_{p_{k} \in \mathcal{P}_{i}} e^{D 2 D}\left(\boldsymbol{p}_{k}, \boldsymbol{T}_{i}^{-1} \boldsymbol{T}_{j}\right) \\ e^{D 2 D}\left(\boldsymbol{p}_{k}, \boldsymbol{T}_{i j}\right) &=\boldsymbol{d}_{k}^{T}\left(\boldsymbol{C}_{k}^{\prime}+\boldsymbol{T}_{i j} \boldsymbol{C}_{k} \boldsymbol{T}_{i j}^{T}\right)^{-1} \boldsymbol{d}_{k} \end{aligned}\\ p_k=(\mu_k,C_k)\\ d_k=\mu'_k-T_{ij}\mu_k\]

1. IMU预积分因子

   通过预积分将IMU约束插入到因子图中，在给定IMU测量的情况下，传感器的未来状态可以估计为：

   \[\begin{aligned} \boldsymbol{R}_{t+\Delta t} &=\boldsymbol{R}_{t} \exp \left(\left(\boldsymbol{\omega}_{t}-\boldsymbol{b}_{t}^{\omega}-\boldsymbol{\eta}_{k}^{\omega}\right) \Delta t\right) \\ \boldsymbol{v}_{t+\Delta t} &=\boldsymbol{v}_{t}+\boldsymbol{g} \Delta t+\boldsymbol{R}_{t}\left(\boldsymbol{a}_{t}-\boldsymbol{b}_{t}^{a}-\boldsymbol{\eta}_{t}^{a}\right) \Delta t \\ \boldsymbol{t}_{t+\Delta t} &=\boldsymbol{t}_{t}+\boldsymbol{v}_{t} \Delta t+\frac{1}{2} \boldsymbol{g} \Delta t^{2}+\frac{1}{2} \boldsymbol{R}_{t}\left(\boldsymbol{a}_{t}-\boldsymbol{b}_{t}^{a}-\boldsymbol{\eta}_{t}^{a}\right) \Delta t^{2} \end{aligned}\\ \eta^a_t和\eta^{\omega}_t都是IMU测量中的白噪声\]

   IMU 预积分因子对两个时间步 i 和 j 之间的相对变化进行积分，以获得相对位姿运动约束：

\[\begin{aligned} \Delta \boldsymbol{R}_{i j} &=\boldsymbol{R}_{i}^{T} \boldsymbol{R}_{j} \exp \left(\delta \phi_{i j}\right) \\ \Delta \boldsymbol{v}_{i j} &=\boldsymbol{R}_{i}^{T}\left(\boldsymbol{v}_{j}-\boldsymbol{v}_{i}-\boldsymbol{g} \Delta t_{i j}\right)+\delta \boldsymbol{v}_{i j} \\ \Delta \boldsymbol{t}_{i j} &=\boldsymbol{R}_{i}^{T}\left(\boldsymbol{t}_{j}-\boldsymbol{t}_{i}-\boldsymbol{v} \Delta t_{i j}-\frac{1}{2} \boldsymbol{g} \Delta t_{i j}^{2}\right)+\delta \boldsymbol{t}_{i j} \end{aligned}\\ \delta\phi_{ij},\delta v_{i,j}和\delta p_{i,j}都是预积分过程中的白噪声\]

IMU预积分因子使系统能够在几何特征不足且 LiDAR 因子可能不足的环境中保持因子图的良好约束。

1. 预处理模块

   我们首先使用体素网格过滤器对输入点云进行下采样。除了对每个体素的位置进行矫正偏移以外，我们还对点的时间戳进行平均化处理。如果一个点的时间戳显著不同于相邻的体素格，该点会被分配给另一个新体素格，以避免错误的融合。然后，为后续点的协方差估计找到 k 个相邻点。我们假设点的邻域关系在接下来的去偏过程中不会发生很大变化，并在去偏之后使用预先计算的最近邻结果进行协方差估计。

2. 里程计估计

   里程计估计模块通过融合 LiDAR 和 IMU 测量来补偿快速传感器运动并稳健地估计传感器状态。首先通过基于 IMU 动力学的运动预测将点转换为 IMU 帧来纠正由传感器运动引起的点云失真。然后我们使用预先计算的相邻点计算每个点的协方差。 在点的偏移矫正完成之后，按照下图构建因子图。

   

   为了限制计算成本并确保系统具有实时能力，使用固定滞后平滑方法并边缘化旧帧。受直接稀疏里程计的启发，作者引入了一种用于高效和低漂移轨迹估计的关键帧机制。关键帧是一组经过选择的帧，它们在空间上分布良好，同时与最新帧有足够的重叠

   为了管理关键帧，我们将两个帧 Pi 和 Pj 之间的重叠率定义为 Pi 中落在 Pj 体素内的点的分数。每次新帧到达时，我们都会评估该帧与最新关键帧之间的重叠率，如果重叠小于阈值（例如，90%），我们将该帧插入到关键帧列表中。使用以下策略删除冗余关键帧：

   A. 删除与最新关键帧重叠小于某个阈值的关键帧

   B. 如果已经存在20个关键帧，删除下式分数最小的关键帧

\[s(i)=o\left(i, N^{\text {odom }}\right) \sum_{j \in\left[1, N^{\text {odom }}-1\right] \backslash\{i\}}(1-o(i, j))\\ o(i,j)代表i帧和j帧的重叠度\]

除了关键帧之外，还在最新帧和最后几帧（例如，最后三帧）之间创建匹配成本因子，以使里程计估计对快速传感器运动具有鲁棒性，另外在连续帧之间还需要创建一个 IMU 预积分因子，以在无特征环境中保持稳健性

1. 局部建图

   一旦从里程计边缘化一个帧，它就会作为传感器状态的初始估计被送到局部建图模块。局部建图模块将多个局部帧合并为一个子图，以减少全局建图模块中优化变量的数量。

   首先使用边缘化状态重新执行点云去偏斜和协方差估计，这将改进在里程计估计开始时所做的初始预测。然后评估该帧与子图中最新帧之间的重叠率，如果重叠率小于阈值（例如，90%），则将该帧插入子图因子图中

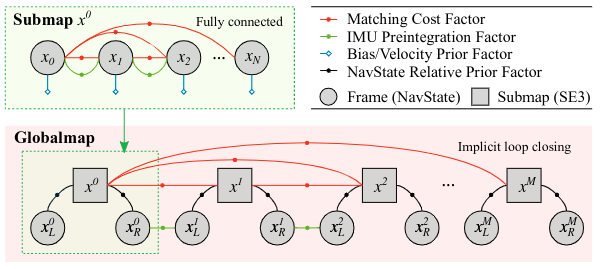
   如下图所示，子图中的每对帧都会创建出一个匹配残差因子，另外因子图中还包括相邻帧的IMU预积分因子和每一帧的速度和偏差的先验因子。一旦子图中的帧数达到阈值或第一帧和最后一帧之间的重叠小于阈值，使用LM优化器执行因子图优化并根据优化结果将帧合并为一个子图

1. 全局建图

   全局建图模块对位姿进行校正以获得全局一致的建图结果。在每个重叠率超过一个小阈值的子图对之间创建一个匹配成本因子。因此会有一个非常密集的因子图。每个子图不仅与图上的相邻子图对齐，而且与每个重新访问的子图对齐，这会产生隐式闭环。

   全局建图模块会以更大的时间间隔（例如，10 秒）创建子图。如果只是在子图之间仅包括IMU 因子，它的不确定性会变得太大，并且它不能强约束子图之间的相对位姿。此外，还会丢失由局部建图模块估计的速度和 IMU 偏差的信息。为了解决这些问题，我们为每个子图$x^i$引入了两个称为端点（$x^i_L$ 和 x^i_R）的状态；它们保存子图中第一帧和最后一帧相对于子图位姿的状态

   假设子图给定$N^{sub}$个传感器状态，那么定义子图的原点位姿为中间状态。那么传感器当前状态相对于子图原点的相对变化可以表述为：

\[\begin{aligned} \boldsymbol{T}_{t}^{\prime} &=\left(\boldsymbol{T}^{i}\right)^{-1} \boldsymbol{T}_{t} \\ \boldsymbol{v}_{t}^{\prime} &=\left(\boldsymbol{R}^{i}\right)^{-1} \boldsymbol{v}_{t} \\ \boldsymbol{b}_{t}^{\prime} &=\boldsymbol{b}_{t} \end{aligned}\]

所以，子图的两个端点关于子图的变化可以用上述公式描述，相邻时间间隔短的帧之间的约束直接通过IMU因子约束，从而可以强约束子图位姿，同时避免局部建图模块估计的速度和偏差信息的丢失。

1. 实验

A. Newer College dataset

实验性能明显优于其他baseline。另外根据作者的描述，在轨迹图的对比中，可以证明快速传感器运动的鲁棒性，因为轨迹中包括了一段动态旋转变化的路径。

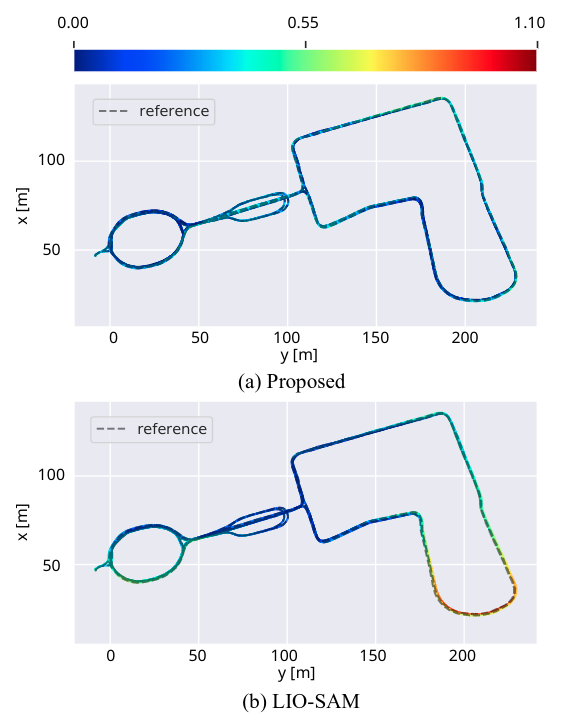
B. KAIST Urban dataset

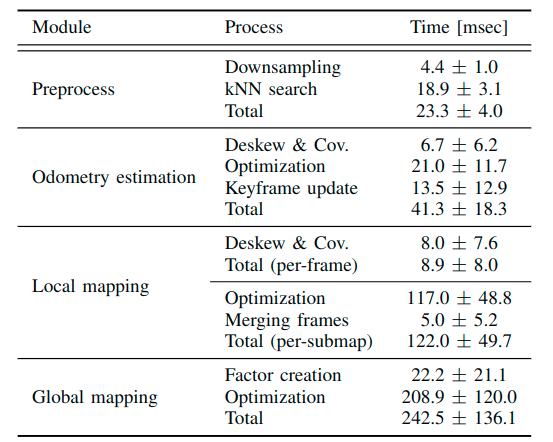
首先是时间分析:可以看出，绝大部分时间消耗来自建图模块，因为那个模块是基于GTSAM进行优化,这一部分并没有GPU加速。

下图是一个建图结果，输出的地图感觉还是挺不错的。

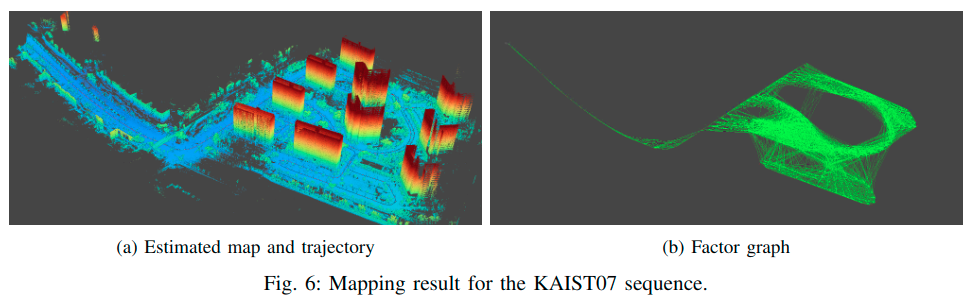
下图分别是不同环境下的实时的处理结果，黄色的部分代表的最新的帧，可以看出在低重叠以及少特征等环境下仍然具有很好的匹配性能。

下图是优化时间，子图数量，残差数量随着时间推移的变化，可以看出，随着运行时间变长，子图和残差数量线性增长，但是优化时间相对稳定。

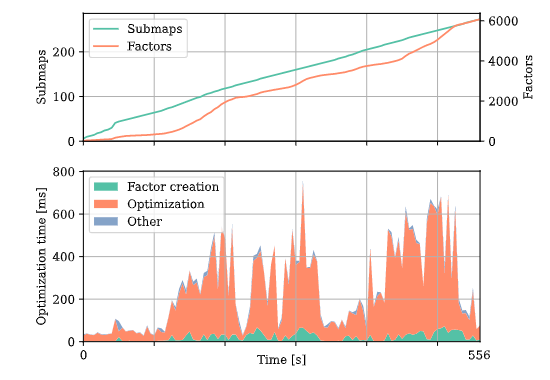
Conclusion

这篇文章的话，解决的问题正如他自己所说，就是解决了后端的LIDAR和IMU的紧耦合问题。后端的融合采用的是局部子图和全局建图的搭配，局部子图将IMU因子，LIDAR因子进行合并输出到全局图，全局图考虑计算成本等因素，重新构建一种因子图，即端点+因子图，端点和因子图之间的优化可以承受时间消耗较大的优化，因子图内部直接采用相邻的IMU约束进行快速更新。总体来讲，这份工作还是不错的。最后，关于GICP用GPU加速的思路也可以进行借鉴，看起来是挺实用的。