这个IRIS的起名，来源于人的虹膜识别信号。虹膜区域内的每个点通常会通过道格曼橡胶板模型映射为一对极坐标，激光雷达的点云同样也可以被映射为极坐标的表示。

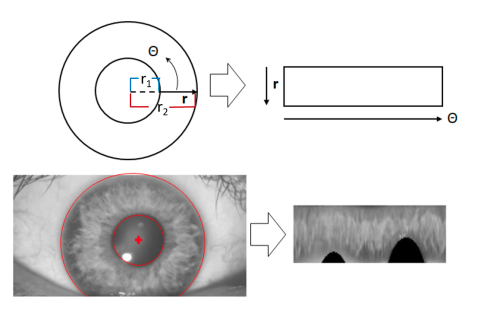
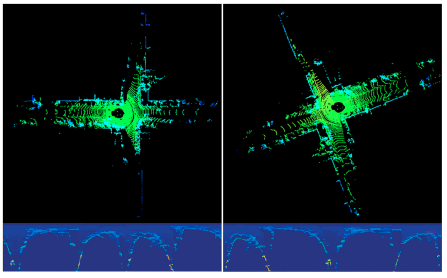
下图是当IRIS检测到回环的时候的候选帧与匹配帧的点云极其对应的IRIS生成图:

本篇论文解读已投稿至3D视觉工坊，记录在个人博客仅供个人学习记录，商业转载行为请联系3D视觉工坊公众号

《LiDAR Iris for Loop-Closure Detection》(IROS 2020 )

Motivation

目前激光的全局或者局部描述子的描述能力和不变性能里仍然有所欠缺，虽然Scan-Context的提出，很大程度上缓解了这个问题，但是Scan-Context本身仍然有一些缺陷，一是它只利用了最大的高度，丢失了很多点云信息，二是Scan-Context不具有旋转不变性，需要进行暴力匹配，三是Scan-Context缺少特征提取步骤。IRIS一一解决了上述缺陷。

Contribution

1. 提出了一个LiDAR点云的全局描述符LiDAR Iris，将一个地方总结为在LiDAR-Iris图像表示上进行几次Gabor过滤和阈值操作后获得的二进制签名图像, 充分利用了点云的大部分信息。
2. 该全局描述符具有旋转不变性，避免了暴力搜索，节约了计算资源。
3. 与现有的LIDAR全局描述符相比，该描述符的性能达到了SOTA。

Content

Lidar Iris描述符的生成理论上可以分解为4个步骤: 一是离散化鸟瞰图像；二是对离散后的图像进行编码；三是生成Lidar-Iris图像；四是对图像执行二值化。执行上可以分解为三个模块，一是生成Lidar-Iris图像的表示；二是通过傅立叶变换使得Lidar-Iris具有平移不变性；三是基于LoG-Gabor滤波器的二值特征提取。

1. Lidar-Iris图像的表示的生成

   首先将点云转换为鸟瞰图，过程示意图如下。具体过程是保留一个面积为k×k的正方形作为有效感应区，激光雷达的位置作为正方形的中心。以这个正方形为单位，将点云离散为80(径向) * 360(角向)的bin。

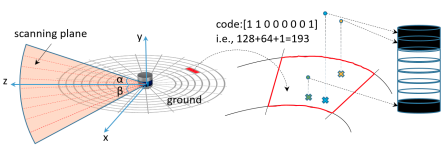
为了完整地表示点云，对每个面元内的点采用一些特征提取方法，如高度、距离、反射、环等。为简单起见，使用八位二进制代码对同一个bin内的所有点进行编码。以高度的编码方法举例，对于每一个bin内的点云集，首先按照高度的大小顺序，线性离散为8个bin，并不是每个bin都会有点，有点的bin值为1，否则为0，从而可以获得上图中的8位二进制编码。

仿照虹膜识别算法，Lidar-IRIS将激光雷达的鸟瞰图扩展为图像条，Lidar-IRIS图像的像素强度为每个bin的8位二进制数所转换的十进制数。一方面，与现有的基于直方图的全局描述符相比，所提出的编码过程不需要对每个bin中的点进行计数，从而提高了计算效率；另一方面，该编码过程是固定的，不需要像CNNs模型那样预训练。这时候的描述子尚未具有平移不变性，下面会通过傅立叶变换使得描述子具有平移不变性。

1. 对于具有平移不变性Lidar-Iris的傅立叶变换

   平移变化会导致基于激光雷达的闭环检测的Lidar-IRIS描述子的显著退化。为了解决这个问题，采用傅里叶变换来估计两幅Lidar-IRIS图像之间的平移。基于傅里叶变换的方案能够估计大的旋转、缩放和平移(用不到缩放)。点云的旋转对应于经过傅里叶变换后的Lidar-IRIS图像的水平平移, 点云的平移不仅对应傅里叶变换后的 LiDAR-Iris 图像的垂直平移，还会引起Lidar-IRIS图像像素强度的轻微变化, 但是Lidar-IRIS以bin为最小单位保留了点云的绝对内部结构，提高了辨别能力并且对图像像素强度的变化具有鲁棒性, 所以可以忽略由机器人在小范围内平移引起的 LiDAR-Iris 图像中强度的变化。

   假设两个Lidar-IRIS图像仅仅差别一个位移:

\[I_{1}(x, y)=I_{2}\left(x-\delta_{x}, y-\delta_{y}\right)\]

那么这两个图像之间的傅立叶变换可以定义为:

\[\hat{I}_{1}\left(w_{x}, w_{y}\right) \dot{e}^{-i\left(w_{x} \delta_{x}+w_{y} \delta_{y}\right)}=\hat{I}_{2}\left(w_{x}, w_{y}\right)\]

对应的，归一化的交叉功率谱定义为:

\[\hat{C o r r}=\frac{\hat{I}_{2}\left(w_{x}, w_{y}\right)}{\hat{I}_{1}\left(w_{x}, w_{y}\right)}==\frac{\hat{I}_{2}\left(w_{x}, w_{y}\right) \hat{I}_{1}\left(w_{x}, w_{y}\right) *}{\left|\hat{I}_{1}\left(w_{x}, w_{y}\right) \hat{I}_{1}\left(w_{x}, w_{y}\right) *\right|}=e^{-i\left(w_{x} \delta_{x}+w_{y} \delta_{y}\right)}\\ *表示复共轭\]

1. 基于LoG-Gabor滤波器的二值特征提取

   使用LoG-Gabor滤波器从Lidar-IRIS图像中深入提取特征: LoG-Gabor滤波器可用于将Lidar-IRIS区域中的数据分解为以不同分辨率出现的分量，与传统的傅里叶变换相比，它的优势在于允许频率数据局部化，允许在相同位置和分辨率进行特征匹配。为了确保实时性，仅使用1D LoG Gabor滤波器。一维Log-Gabor滤波器的频率响应如下:

\[G(f)=\exp \left(\frac{-\left(\log \left(f / f_{0}\right)\right)^{2}}{2\left(\log \left(\sigma / f_{0}\right)\right)^{2}}\right)\\ f_0给出了滤波器的中心频率，\sigma影响滤波器的带宽，并且\sigma/f_0需要保持常数值。\]

利用八个1D LoG Gabor滤波器对Lidar-IRIS图像的每一行进行卷积，其中滤波器的波长增加相同的因子，从而得到每个滤波器的实部和虚部。在下图中，第一幅图像显示了八个1D log-Gabor滤波器，第二幅图像显示了前四个滤波器卷积响应的实部和虚部:

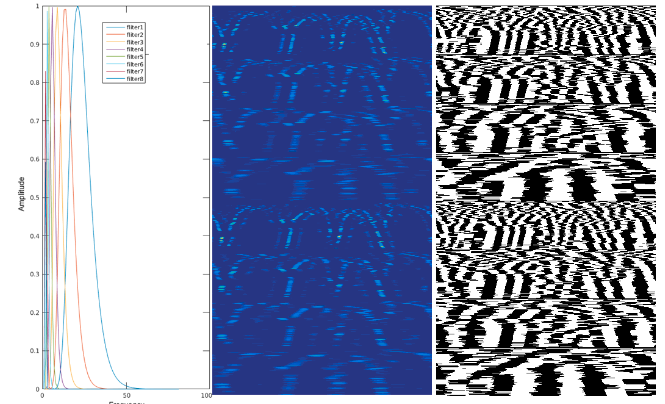
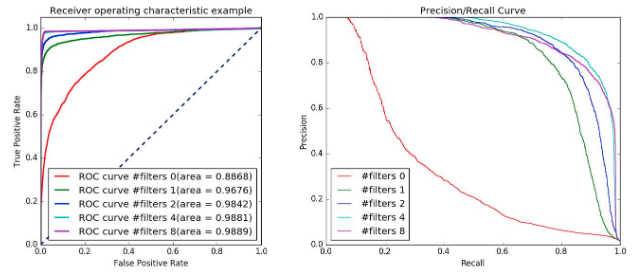
尝试使用不同数量的LoG-Gabor滤波器进行特征提取，实验中发现四个LoG-Gabor滤波器可以在较低的计算成本下实现最佳的闭环检测精度。下图显示了使用不同数量的LoG-Gabor滤波器可以在验证集上实现的精度，其中使用四个滤波器的结果是最好的。通过简单的阈值运算，将四个滤波器的卷积响应转化为二值，从而将它们叠加到每个Lidar-IRIS图像的大型二值特征图中。上图的第三幅图像显示了激光雷达虹膜图像的一个二值特征图。

1. 使用Lidar-IRIS的闭环检测

   为了将Lidar-IRIS应用于闭环检测，为每个点云生成一个Lidar-IRIS的二值特征图。因此，可以保存所有关键帧获取的Lidar-IRIS二进制特征的历史数据库。当前关键帧和每个历史关键帧的Lidar-IRIS二值特征贴图之间的距离由汉明距离计算。如果获得的汉明距离小于阈值，则将其视为环路闭合事件

2. 实验结果

A. 亲和矩阵可视化

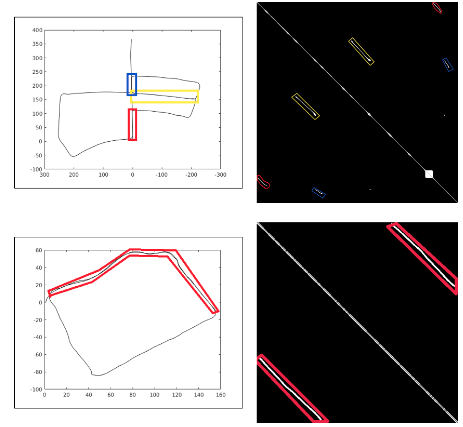
第一行表示KITTI05的数据集，第二行表示作者自己采集的小规模数据集，第一列表示真值生成的亲和矩阵，第二列到第五列分别表示Lidar-IRIS，ScanContext，M2DP和ESF生成的亲和矩阵。在Lidar-IRIS和ScanContext的亲和矩阵里，颜色越重，相似度越高，在M2DP和ESF的亲和矩阵里，颜色越轻，相似度越高。

B. 对应A的轨迹

对应于上述闭环的亲和矩阵放大和对应的轨迹。

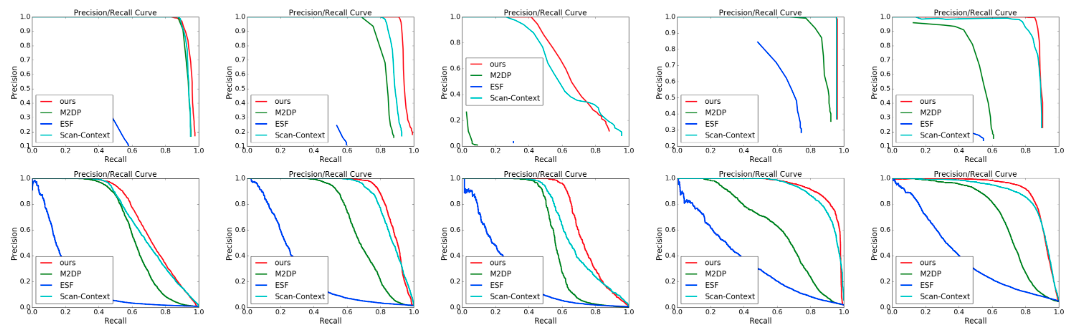
C. 准确率-召回率取线

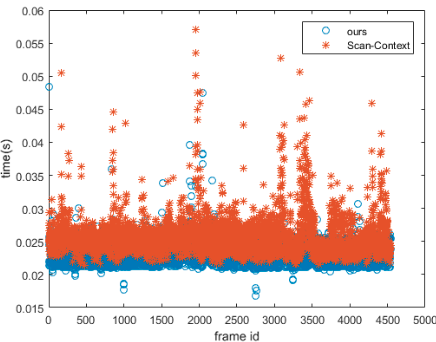
D. 时间对比

主要和Scan-Context对比每帧所需要的时间，数据集是KITTI00。

Conclusion

Lidar-IRIS和Scan-Context的思路是比较相似的，总体上对Scan-Context进行了改进，一是改进了Scan-Context只利用了点云最大高度的问题，二是解决了Scan-Context对于平移不变性需要使用暴力搜索的问题，论文中的实验性能明显高于Scan-Context，实际效果需要运行后测试。