基于图论的点云数据关联方法,通过寻找最稠密的子图来寻找一致关联(内联),通过投影梯度上升的方法保持低时间复杂度,在斯坦福兔子的嘈杂点与990个异常值关联和仅10个内部关联关联关联的实例中,该方法成功地在138毫秒内以100%的精度返回了8个内部关联。
代码已开源: https://mit-acl.github.io/clipper
本篇论文解读已投稿至3D视觉工坊,记录在个人博客仅供个人学习记录,商业转载行为请联系3D视觉工坊公众号
《CLIPPER: A Graph-Theoretic Framework for Robust Data Association》(ICRA 2021 )
Motivation
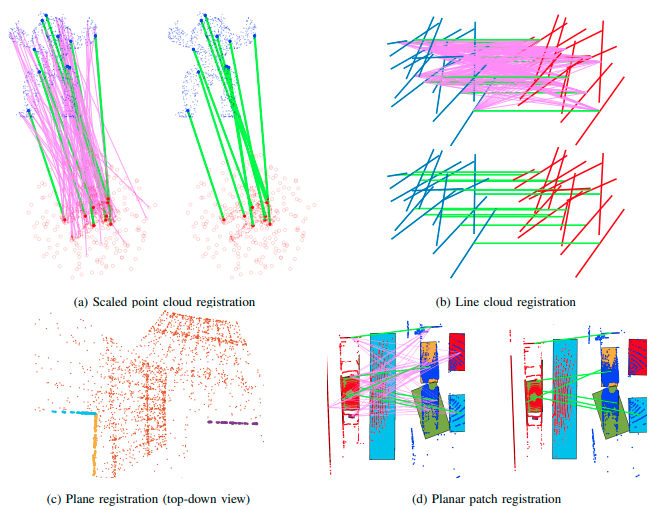
点云匹配问题的传统解决方法是基于高相似性对应对象的传统线性分配方法,例如匈牙利法或拍卖算法,对高噪声、高离群值区域不具有鲁棒性,从而会产生不正确的对应。为了提高匹配算法的鲁棒性和精确度,作者提出了CLIPPER(一致性连接、剪枝和匹配错误矫正)框架,该框架利用对象对之间的几何一致性概念,可以在极端的离群点存在的情况下下找到正确的对应关系。下图是CLIPPER算法在不同匹配需求中的应用。
Contribution
- 提出了一种适用于二元图和加权图的内联关联选择优化公式。
- 提出了具有最优性保证的NP难优化问题的松弛形式。
- 提出了一种多项式时间算法,用于求解基于投影梯度上升的松弛公式,可扩展到大型数据关联问题。
Content
-
一致性图框架
在有大量离群值和噪声的情况下进行鲁棒数据关联的过程可以通过一致性图框架描述。点云配准问题的目标是找到两组点云之间的旋转和平移 ,点云点之间关联的一致性可以在一致性图的图论框架中进行评估和表示: 包含有n个关联对的一致性图G有n个顶点,即每个顶点都表示一个关联对,顶点之间的边表示关联对间的一致性。下图展示出了从点云中抽取出一致性关联图的过程:
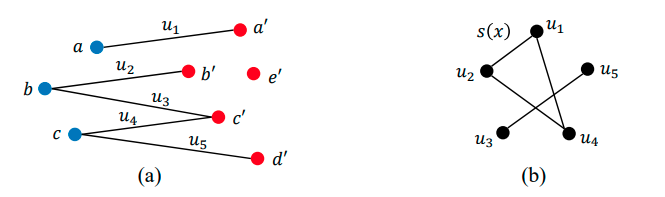
由于旋转和平移是保持距离的变换,因此当关联正确时,一个集合中的点之间的距离应与另一个集合中的点之间的距离相同(在无噪假设中),这个性质可用于评估两个关联的几何一致性,其中G的两个顶点之间的边表示关联匹配的点之间的距离相同,最终上图中的u1,u2,u4被视为是相互关联的匹配对。
-
亲和矩阵
一个有n个顶点的一致性图的亲和矩阵M是一个nxn的对陈矩阵。对陈线上的值M(i,i)表示关联i匹配对的数据点之间的相似性,当相似性信息未知的情况下,对陈线的值全部设为1,在这种情况下,M=A+I, A是一致性图的权重邻接矩阵。M(i,j)表示第i个匹配对和第j个匹配对之间的几何一致性(在点云匹配任务中,匹配点之间的距离可以用作几何一致性的验证),最终生成的亲和矩阵如下:
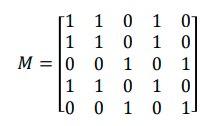
-
Clipper算法的优化方程
给定代表关联对的一致性图和它的亲和矩阵后,提出优化问题用于查找一致关联的最密集子集:
因为M是二分矩阵,所以上述问题可以简化为一个最大团问题(MCP问题):
\[\begin{array}{cl} \underset{u \in\{0,1\}^{n}}{\operatorname{maximize}} & \sum_{i=1}^{n} u_{i} \\ \text { subject to } & u_{i} u_{j}=0 \quad \text { if } M(i, j)=0, \forall_{i, j} \end{array}\]因为MCP问题是一个NP问题,因此,随着问题规模的增长,依赖于求解上述优化形式的算法在计算上变得难以处理。
将图的密度定义为边权重的总和除以顶点数。最稠密子图是图顶点及其对应边的子集,这些顶点及其对应边具有最高密度。给定一个具有亲和矩阵M(具有1个对角项)的图G ,G 的最稠密子图可从如下公式获得:
\[{maximize}_{u \in\{0,1\}^{n}} \frac{u^{\top} M^{\prime} u}{u^{\top} u}\]可以发现这个形式和第一个优化问题形式很相似,所以第一个优化问题形式也可以被解释为找到一致性连通图G的最密集的完全连通的子图。最密集的子图目标在加权情况下很有用,但是需要与最大边加权团问题区分开来,例如,考虑一个加权矩阵M和两个解的候选U,U’:
\[M=\left[\begin{array}{ccccc} 1 & 1 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0.2 & 0.2 \\ 0 & 0 & 0.2 & 1 & 0.2 \\ 0 & 0 & 0.2 & 0.2 & 1 \end{array}\right], u=\left[\begin{array}{l} 1 \\ 1 \\ 0 \\ 0 \\ 0 \end{array}\right], \bar{u}=\left[\begin{array}{l} 0 \\ 0 \\ 1 \\ 1 \\ 1 \end{array}\right]\]U’是MCP问题形式的解,但是U‘在矩阵M中对应的一致性分数很低,大致在0.2左右,所以在亲和矩阵中通过加权方案进行选择子图是很好重要的,否则很容易选到低一致性的子图。
求解第一个公式的主要挑战是由于问题的二元域和包含u的非线性目标函数导致的问题的组合复杂性,这主要导致在时间有限的情况下很难获得全局最优解,即使是小规模的点云。一个标准的解决方法是放宽二元域和公式一的约束,以获得适合快速求解的连续问题,然后将此解投影回原始问题的域并且约束流形,本文中作者提出的公式一的放宽松弛形式如下:
\[\begin{array}{ll} \underset{u \in \mathbb{R}^{n}}{\operatorname{maximize}} & F(u) \stackrel{\text { def }}{=} u^{\top} M_{d} u \\ \text { subject to } & \|u\| \leq 1 \end{array}\] \[M_{d}(i, j) \stackrel{\text { def }}{=}\left\{\begin{array}{ll} M(i, j) & \text { if } M(i, j) \neq 0 \\ -d & \text { if } M(i, j)=0 \end{array}\right.\]直观地说,当Md(i,j) = −d时,标量d惩罚目标中ui,uj的联合选择量为−2d * ui * uj。因此,随着 d 的增加,违反约束的u的数量为零。当d>=n的时候,上述形式的解会满足公式一的约束,即当M(i,j)=0的时候ui * uj=0。
由于公式一是一个NP问题,因此根据初始条件,用于求解公式五的优化算法可能会收敛到局部最优。为了保证找到全局最优,需要搜索整个解空间。
-
CLIPPER算法
CLIPPER算法包括两个步骤, 一是通过使用回溯跟踪线搜索的投影梯度上升方法获得公式5的解u; 二是通过选择 ˆω 最大元素来估计 u 中最密集的聚类,算法伪代码如下:

上述算法通过递增惩罚参数 d( 13 行)并通过梯度上升(7-12 行)求解公式五来寻求可行的子图。 首先投影到u(第9行)到Sn的切线上,并根据这个正交投影移动,为了在搜索空间中快速移动,贪婪地选择α步长,以便如果有ui要惩罚,渐变步长会导致结果达到正序的边界(10 行)。在任何一种情况下,如果选择α太大,则使用回溯行搜索来查找适当的步骤( 11 行)。解被投影回约束流形(12行),梯度上升继续。
CLIPPER的最后一步选择子图G′(14-15行)中最密集的分量,由于对于所有 Md(i,j) = −d 元素 ui,uj 在解u中满足 ui uj = 0,然后,最密集分量的顶点被标识为 U 中最大的 ˆω 元素。
- 实验结果
误差规模变化:
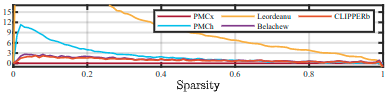
时间变化
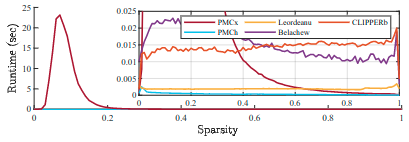
斯坦福兔子点云

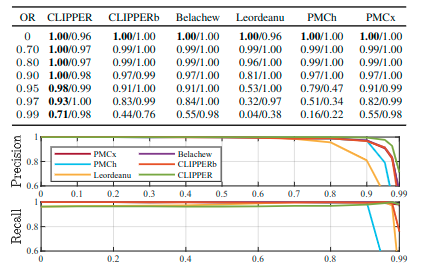
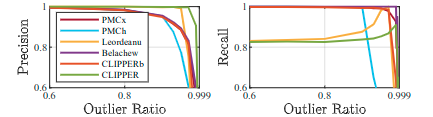
不同参数下的精确率与召回率
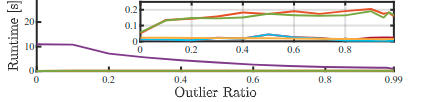
离群点比例和运行时间的关联
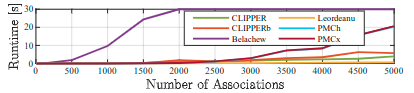
关联对和运行时间的关联
离群点比例和精确率召回率的关联
Conclusion
这篇文章使用几何一致性概念的鲁棒数据关联的图理论框架解决点云匹配有问题。实验证明能够以低运行时间始终如一地执行,并超越最先进的技术,在99%的异常值条件下实现100%的精度,80%的召回率。总体来讲是很不错的,但是具体应用在SLAM中的效果有待尝试。
