基于视觉的线面特征融合方案

《Plane-Edge-SLAM: Seamless Fusion of Planes and Edges for SLAM in Indoor Environments》(TASE-2020 )

Motivation

平面特征和边特征在室内场景里是非常有用的特征，但是目前想要无缝融合这两个特征仍然是一个挑战(关于无缝融合的定义，读完论文，我认为作者想要表达的是一个实时权重调整的特性，论文的特征主体是面特征，论文里做的是线特征的权重根据面特征的一些置信度概率来实时调整)

Contribution

1.提出了一种平面与边缘的无缝融合来充分约束运动估计。在融合过程中，充分利用了平面和边缘所提供的约束条件。无缝融合使得运动估计问题在任何情况下都保持良好的适定性，也为特征融合问题提供了一个新的视角。 2.分析了平面约束对摄像机运动估计的影响，导出了约束运动子空间的显式表示。提出了一种定量测量给定摄像机运动约束强度的方法。分析结果不仅可用于平面和边缘的融合，也可用于运动估计奇异解的识别。 3.提出了一种概率平面拟合算法，利用深度图像中的噪声点来拟合平面模型。所估计的平面模型对测量噪声具有较强的适应性，有利于基于平面的摄像机运动估计

Content

1. 系统框图

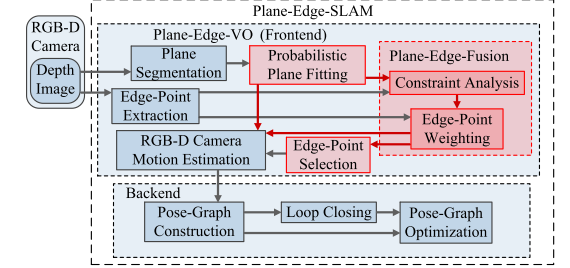
   如下图所示，两种特征都是通过RGB-D传感器获取的。在概率平面拟合模块中，对每个平面段的噪声点进行平面模型拟合。然后通过约束分析和边缘点加权两个子模块进行两个特征的融合。

   在约束分析模块中，导出了约束运动子空间的显式表示。边缘点加权模块利用约束分析的结果，自适应地为边缘点分配不同的权重。

1. 平面概率拟合

   从点云中分割平面区域并将不定平面模型拟合到每个平面区域，论文采用基于统计信息网格的方法对平面区域进行分割。根据论文引用参考文献的段落表明，对于深度传感器而言(包括激光传感器和RGB-D传感器)，所以，因此，在拟合平面时，应考虑两个方面：首先，估计的平面模型应该更适合测量更精确的点；其次，不确定度需要从深度和像素测量传播到点到平面的距离。

   首先，通过作者在之前论文提出的基于统计学习的方法分割点云，分割出的点云定义为:

\[\left\{\boldsymbol{p}_{\pi j}\right\}_{j=1, \ldots, N_{p \pi}}\]

假设噪声符合一个零均值的高斯模型，那么协方差可以定义为:

\[\begin{aligned} \boldsymbol{C}_{p_{\pi j}}=&\left(\boldsymbol{K}^{-1} \tilde{\boldsymbol{u}}_{j}\right) \sigma_{z j}^{2}\left(\boldsymbol{K}^{-1} \tilde{\boldsymbol{u}}_{j}\right)^{T} \\ &\left.+\left(z_{j} \boldsymbol{k}_{1}\right) \sigma_{u j}^{2}\left(z_{j} \boldsymbol{k}_{1}\right)^{T}+\left(z_{j} \boldsymbol{k}_{2}\right) \sigma_{v j}^{2}\left(z_{j} \boldsymbol{k}_{2}\right)^{T}\right) \end{aligned}\]

（不同的传感器的噪声测量模型是不同的，这个仅仅是RGB-D的噪声测量模型，但是无论是什么传感器，都适用于文章中提出的概率平面拟合方法）:

拟合的平面定义和点面距离定义如下:

\[\boldsymbol{\pi}=\left[\boldsymbol{n}^{T}, d\right]^{T}\\ l_{\pi j}=\boldsymbol{n}^{T} \boldsymbol{p}_{\pi j}+d\]

点面的距离同样符合0均值高斯分布，方差是:

\[\sigma_{l \pi j}^{2}=\frac{\partial l_{\pi j}}{\partial \boldsymbol{p}_{\pi j}}^{T} \boldsymbol{C}_{p_{\pi j}} \frac{\partial l_{\pi j}}{\partial \boldsymbol{p}_{\pi j}}=\boldsymbol{n}^{T} \boldsymbol{C}_{p_{\pi j}} \boldsymbol{n}\]

通过马氏距离的平方来进行优化:

\[D_{l}^{2}\left(l_{\pi j}, \boldsymbol{n}, d\right)=\frac{l_{\pi j}^{2}}{\sigma_{l \pi j}^{2}}=\frac{\left(\boldsymbol{n}^{T} \boldsymbol{p}_{\pi j}+d\right)^{2}}{\boldsymbol{n}^{T} \boldsymbol{C}_{p_{\pi j}} \boldsymbol{n}}(马氏距离的平方)\\ E(\boldsymbol{n}, d)=\sum_{j=1}^{N_{p \pi}} D_{l}^{2}\left(l_{\pi j}, \boldsymbol{n}, d\right)\]

可以求得此处最优d:

\[d^{*}=-\boldsymbol{n}^{T} \boldsymbol{p}_{G}(\boldsymbol{n})\\ \boldsymbol{p}_{G}(\boldsymbol{n})=\frac{\sum_{j=1}^{N_{p \pi}} c_{j}(\boldsymbol{n}) \boldsymbol{p}_{\pi j}}{\sum_{i=1}^{N_{p \pi}} c_{j}(\boldsymbol{n})} \quad c_{j}(\boldsymbol{n})=\left(\boldsymbol{n}^{T} \boldsymbol{C}_{p_{\pi j}} \boldsymbol{n}\right)^{-1}\]

然后可以获得针对n的优化：

\[E(\boldsymbol{n})=\boldsymbol{n}^{T} \boldsymbol{S}(\boldsymbol{n}) \boldsymbol{n}\\ \boldsymbol{S}(\boldsymbol{n})=\sum_{j=1}^{N_{p \pi}} c_{j}(\boldsymbol{n})\left(\boldsymbol{p}_{\pi j}-\boldsymbol{p}_{G}(\boldsymbol{n})\right)\left(\boldsymbol{p}_{\pi j}-\boldsymbol{p}_{G}(\boldsymbol{n})\right)^{T}\]

S(n)可以被视为一个加权映射矩阵，pG(n)是加权质心，可以得到:

\[\begin{array}{l} \boldsymbol{n}^{*}=\arg \min _{n} \boldsymbol{n}^{T} \boldsymbol{S}\left(\boldsymbol{n}_{\mathrm{LS}}\right) \boldsymbol{n} \\ \boldsymbol{p}_{G_{-} \mathrm{LS}}=\frac{1}{N_{p \pi}} \sum_{j=1}^{N_{p \pi}} \boldsymbol{p}_{\pi j} . \boldsymbol{S}_{\mathrm{LS}}=\sum_{j=1}^{N_{p \pi}}\left(\boldsymbol{p}_{\pi j}-\boldsymbol{p}_{G_{-} \mathrm{LS}}\right)\left(\boldsymbol{p}_{\pi j}-\boldsymbol{p}_{G_{-} \mathrm{LS}}\right)^{T} \end{array}\]

事实上，平面参数的不确定性也可以通过优化的海塞矩阵来表示:

\[\boldsymbol{C}_{\pi}^{-1}=\left.\left[\begin{array}{cc} \frac{\partial^{2} E}{\partial \boldsymbol{n}^{2}} & \frac{\partial^{2} E}{\partial d \partial \boldsymbol{n}} \\ \frac{\partial^{2} E}{\partial \boldsymbol{n} \partial d} & \frac{\partial^{2} E}{\partial d^{2}} \end{array}\right]\right|_{n^{*}, d^{*}}=\sum_{j=1}^{N_{p \pi}} c_{j}\left[\begin{array}{cc} \boldsymbol{p}_{\pi j} \boldsymbol{p}_{\pi j}^{T} & \boldsymbol{p}_{\pi j} \\ \boldsymbol{p}_{\pi j}^{T} & 1 \end{array}\right] .\]

1. 无缝融合两种特征

   每个边缘点对代价函数的贡献是根据平面提供的约束自适应调整的。因此，将边缘信息与平面融合，确定摄像机运动的所有分量。下面是基于面-线特征的位姿估计的代价函数:

\[\begin{array}{l} F(\boldsymbol{\xi})=\sum_{i=1}^{N_{\pi}} \boldsymbol{e}_{\pi i}^{T} \boldsymbol{\Omega}_{\pi i} \boldsymbol{e}_{\pi i}+W_{p} \sum_{k=1}^{N_{p}} w_{p k} \boldsymbol{e}_{p k}^{T} \boldsymbol{\Omega}_{p k} \boldsymbol{e}_{p k} \\ \boldsymbol{e}_{\pi i}={ }^{c} \boldsymbol{\pi}_{i}-T\left({ }^{r} \boldsymbol{\pi}_{i}, \boldsymbol{\xi}\right) \\ T\left({ }^{r} \boldsymbol{\pi}_{i}, \boldsymbol{\xi}\right)_{\text {表示平面通过这个运动变换的过程 }} \\ T\left({ }^{r} \boldsymbol{\pi}_{i}, \boldsymbol{\xi}\right)=\left[\begin{array}{cc} \boldsymbol{R} & \mathbf{0}_{3 \times 1} \\ -\boldsymbol{t}^{T} \boldsymbol{R} & 1 \end{array}\right]\left[\begin{array}{l} { }^{r} \boldsymbol{n}_{i} \\ r^{r} \end{array}\right] \end{array} \boldsymbol{\Omega}_{\pi \text { 是残差量的信息矩阵(通过 }^{c} \boldsymbol{C}_{\pi i}+{ }^{r} \boldsymbol{C}_{\pi i} \text { 的逆矩阵获得) }}\]

相似的，下面是线特征的相关参数解释:

\[\begin{array}{c} \boldsymbol{e}_{p k}={ }^{\boldsymbol{p}} \boldsymbol{p}_{k}-T\left({ }^{r} \boldsymbol{p}_{k}, \boldsymbol{\xi}\right) \\ T\left({ }^{r} \boldsymbol{p}_{k}, \boldsymbol{\xi}\right)=\boldsymbol{R} \cdot{ }^{r} \boldsymbol{p}_{k}+\boldsymbol{t} \end{array}\]

这个代价函数创新的一点是权重的加入:

\[\begin{array}{l} w_{p k}=\sum_{l=1}^{6} \frac{v_{p k l}}{v_{\pi l}}=\sum_{l=1}^{6} \frac{\lambda_{p k l} / \sum_{k=1}^{N_{p}} \lambda_{p k l}}{\exp \left(\alpha \sqrt{\frac{\lambda_{\pi l}}{\lambda_{\pi 1}}}\right)} \\ W_{p}=\frac{\sum_{l=1}^{6} \lambda_{\pi l}}{\sum_{l=1}^{6} \sum_{k=1}^{N_{p}} w_{p k} \lambda_{p k l}} \\ \lambda_{p k l}=\boldsymbol{q}_{\pi l}^{T} \boldsymbol{\Psi}_{p k} \boldsymbol{q}_{\pi l} \cdot \boldsymbol{\Psi}_{p k}=\boldsymbol{J}_{p k}^{T} \boldsymbol{\Omega}_{p k} \boldsymbol{J}_{p k_{1}} \\ \boldsymbol{J}_{p k}=\frac{\partial \boldsymbol{e}_{p k}}{\partial \boldsymbol{\xi}}=\left[\begin{array}{ll} -\boldsymbol{I}_{3 \times 3} & \left.\left(\boldsymbol{R} \cdot{ }^{r} \boldsymbol{p}_{k}\right)^{\wedge}\right] \\ \Omega_{p k} & =\left({ }^{c} \dot{\boldsymbol{C}}_{p k}+{ }^{r} \boldsymbol{C}_{p k}\right)^{-1} \end{array}\right. \end{array}\]

1. 实验结果

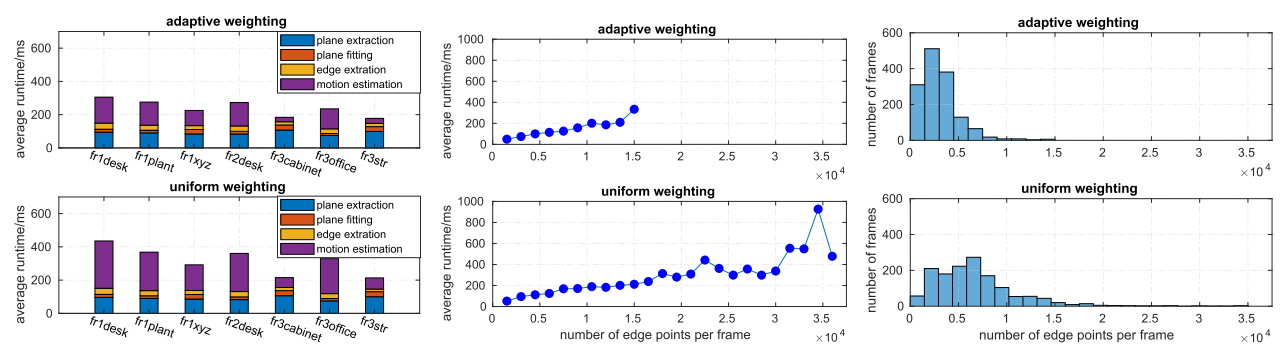
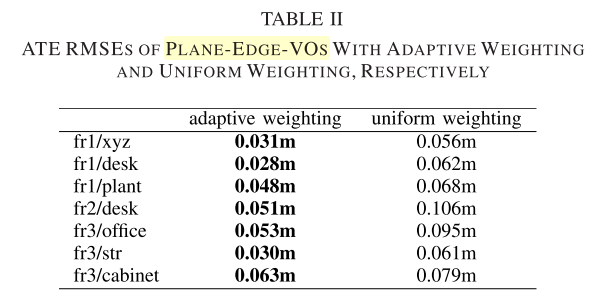
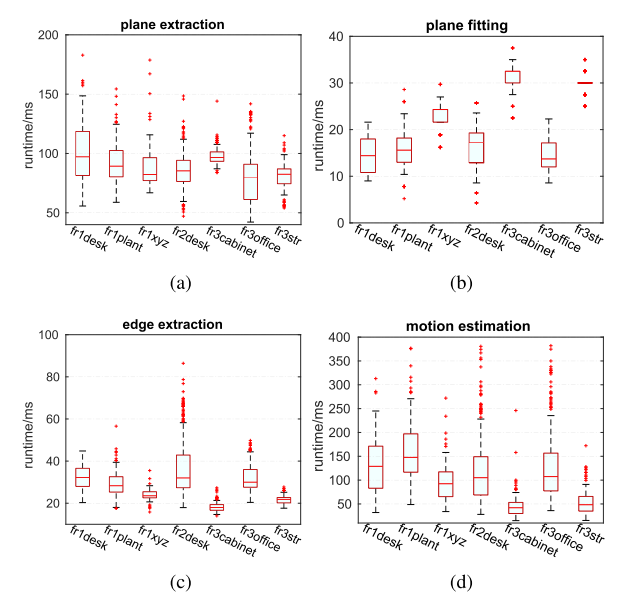
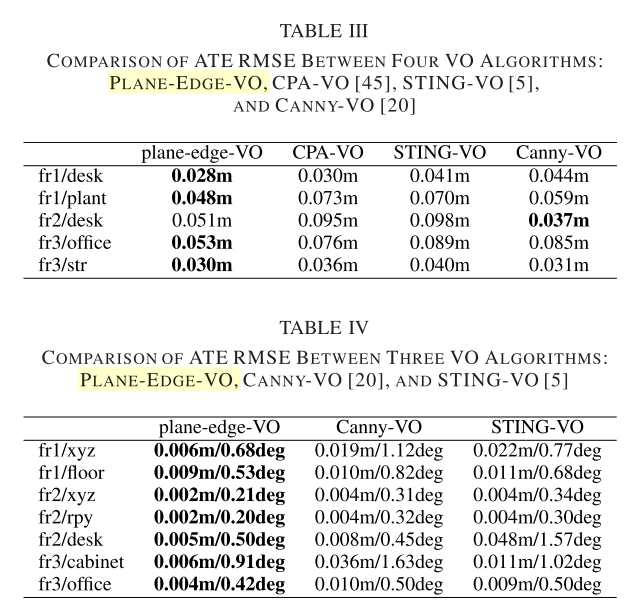
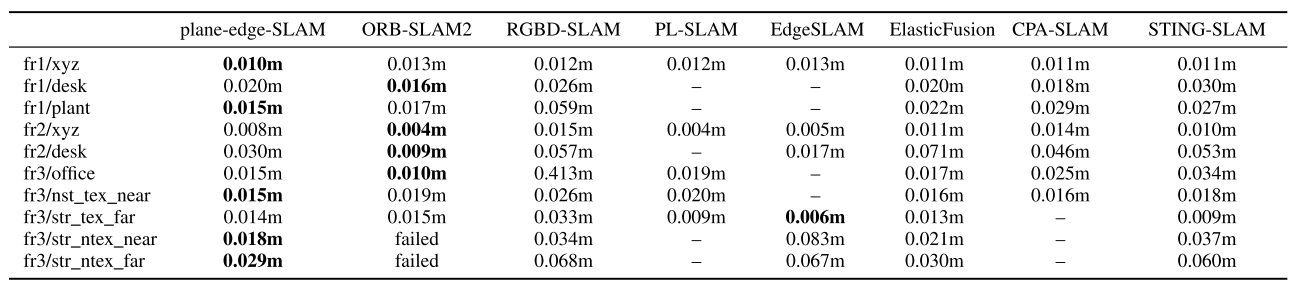
Conclusion

本文的主要创新点在于两个部分，都比较solid，一是将平面模型拟合到测量点。平面拟合利用深度传感器的误差模型，适应不同深度值对应的各种测量噪声。因此，估计的平面模型对于大的测量噪声更加准确和鲁棒。拟合平面进一步用于相机运动的估计，可以大大提高运动估计的准确性。二是精心设计了一种自适应加权算法，用于平面和边缘的无缝融合，边缘点的权重是基于对沿运动空间每个维度的运动的约束强度的定量测量来自适应计算的。