KITTI榜单第14名的方法

《MULLS: Versatile LiDAR SLAM via Multi-metric Linear Least Square》(ICRA2021 )
Motivation
一是目前现有的激光SLAM算法缺乏通用性,难以在工业场景应用,二是绝大多数的激光SLAM算法依赖于点云的组织方式,比如说环(ring)等,三是现有的激光SLAM算法不适用与新型的激光雷达(窄视角的机械雷达和固态雷达),四是目前很多激光SLAM算法都被设计来解决特定场景(城市道路,高速,隧道)的应用,这很容易陷入局部最小值。 为了解决上述问题,作者提出了多尺度最小二乘的激光SLAM方法。
Contribution
- 提出了一个独立于扫描线的激光SLAM方案,在不同的场景都具有低漂移实时的性能,在论文发布的时候,方法在KITTI榜单上排名前十。
- 提出了一种高效的点云局部配准算法MULLS-ICP,实现了粗分类几何特征点中点对点(平面、线)误差度量的线性最小二乘优化。
Content
-
运动补偿
这个方法同样考虑帧内运动, 每个点具有自己的时间戳:
在没有IMU的情况下通过匀速运动差值处理:
\[\mathbf{p}_{i}^{(e)}=\mathbf{R}_{e, i} \mathbf{p}_{i}+\mathbf{t}_{e, i} \approx {slerp}\left(\mathbf{R}_{e, b}, s\right) \mathbf{p}_{i}+s \mathbf{t}_{e, b}\]-
系统详解
框图如下, 输入是原始点云,输出是六类携带主向量和法向量的特征点。
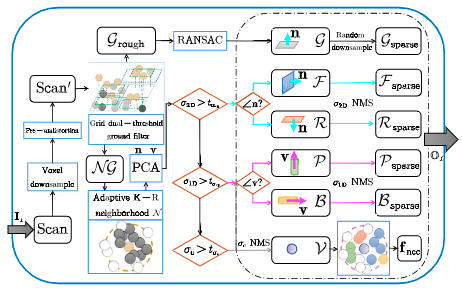
第一步是进行双阈值滤波,预处理(可选)后的点云投影到参考平面,平面是水平的或者是从上一帧的地面点进行拟合,参考平面分成等格的2D体素格,记录下每个体素格内的最小的点高度和对应的三维的邻居体素格,并且可以根据这两个值的大小判定该点是否属于地面点, 并且使用RANSAC来进一步优化拟合地面点。
\[p_{k}^{(i)} \in\left\{\begin{array}{l} \mathcal{N} \mathcal{G}, \text { if } h_{k}-h_{\min }^{(i)}>\delta h_{1} \text { or } h_{\min }^{(i)}-h_{\text {neimin }}^{(i)}>\delta h_{2} \\ \mathcal{G}_{\text {rough }}, \text { otherwise } \end{array}\right.\]第二步是基于PCA的非地面点分类,N为当前点的球形邻域,N的协方差C被定义为:
\[\mathbf{C}=\frac{1}{|\mathcal{N}|} \sum_{i \in \mathcal{N}}\left(\mathbf{p}_{i}-\overline{\mathbf{p}}\right)\left(\mathbf{p}_{i}-\overline{\mathbf{p}}\right)^{\top}\\ \overline{\mathbf{p}}是邻域的重心中心\]然后通过特征值分解获得三个从大到小的特征值 $\lambda_1,\lambda_2,\lambda_3$ 及其对应的特征向量 $v,m,n$ ,最大的特征值对应的向量是主向量,最小的特征值对应的向量是法向量。
相应的该点的局部线形度,平面度,曲率,分别定义为:
\[\sigma_{2 \mathrm{D}}=\frac{\lambda_{1}-\lambda_{2}}{\lambda_{1}}, \sigma_{2 \mathrm{D}}=\frac{\lambda_{2}-\lambda_{3}}{\lambda_{1}}, \sigma_{\mathrm{c}}=\frac{\lambda_{3}}{\lambda_{1}+\lambda_{2}+\lambda_{3}}\]根据主向量&法向量的方向和线形度&平面度&曲率的大小,可以分类成五类特征点,即: 正面(F), 屋顶(R), 支柱(P), 光束(B)和顶点(V);一般而言,线性点有(P,B), 平面点有(F,R), 顶点不属于线性也不属于平面。
第三步是邻居分类语义编码
用来描述顶点关键点,编码邻域内不同类别特征点的比例,归一化强度和离地高度:
\[\mathbf{f}_{\mathbf{i}}^{(\mathrm{ncc})}=\left[\frac{\left|\mathcal{F}_{\mathcal{N}}\right|}{|\mathcal{N}|} \quad \frac{\left|\mathcal{P}_{N}\right|}{|\mathcal{N}|} \quad \frac{\left|\mathcal{B}_{N}\right|}{|\mathcal{N}|} \quad \frac{\left|\mathcal{R}_{\mathcal{N}}\right|}{|\mathcal{N}|} \quad \frac{\bar{I}_{\mathcal{N}}}{I_{\max }} \quad \frac{h_{\mathcal{G}}}{h_{\max }}\right]_{i}^{\mathrm{T}}\]第四步是多尺度线性最小二乘的ICP
这一步的具体流程如下图, 输入是由多类点云特征组成的源点云和目标点云,经过ICP计算后,输出是相对位姿和精确度评价指标:
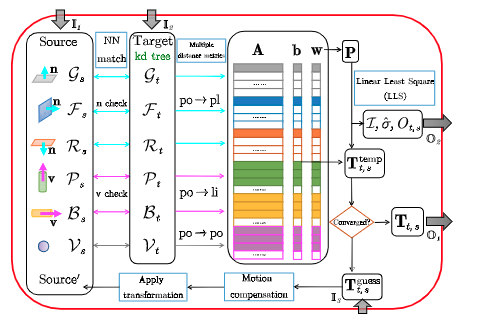
简单来说先是通过最近邻搜索关联点,然后通过主向量和法向量做方向一致性检查,两个对应点的残差定义为:
\[\mathbf{r}_{i}=\mathbf{q}_{i}-\mathbf{p}_{i}^{\prime}=\mathbf{q}_{i}-\left(\mathbf{R} \mathbf{p}_{i}+\mathbf{t}\right)\]具体到点点,点线,点面误差如下:
\[d_{i}^{\mathrm{po} \rightarrow \mathrm{po}}=\left\|\mathbf{r}_{i}\right\|_{2}, \\ d_{j}^{\mathrm{po} \rightarrow \mathrm{pl}}=\mathbf{r}_{j} \cdot \mathbf{n}_{j},\\ d_{k}^{\mathrm{po} \rightarrow \mathrm{li}}=\left\|\mathbf{r}_{k} \times \mathbf{v}_{k}\right\|_{2}\]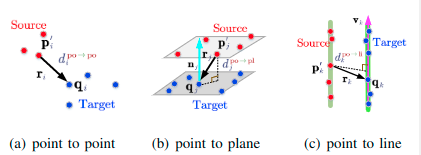
所以优化形式如下:
\[\begin{array}{c} \left\{\mathbf{R}^{*}, \mathbf{t}^{*}\right\}=\underset{\{\mathbf{R}, \mathbf{t}\}} \sum_{i} w_{i}\left(d_{i}^{\mathrm{po} \rightarrow \mathrm{po}}\right)^{2}+\sum_{j} w_{j}\left(d_{j}^{\mathrm{po} \rightarrow \mathrm{p} 1}\right)^{2} \\ +\sum_{k} w_{k}\left(d_{k}^{\mathrm{po} \rightarrow \mathrm{li}}\right)^{2} \end{array}\]在小角度的假设下,R可以被近似为:
\[\mathbf{R} \approx\left[\begin{array}{ccc} 1 & -\gamma & \beta \\ \gamma & 1 & -\alpha \\ -\beta & \alpha & 1 \end{array}\right]=\left[\begin{array}{l} \alpha \\ \beta \\ \gamma \end{array}\right]_{\times}+\mathbf{I}_{3}\]根据高斯马尔科夫参数估计的求解方式, 定义求解形式如下:
\[\mathbf{e}=\mathbf{A} \xi-\mathbf{b}\]整体设计矩阵和观察向量分别定义如下:
\[\begin{aligned} \mathbf{A} &=\left[\begin{array}{lllll} \mathbf{A}_{i}^{\mathrm{po} \rightarrow \mathrm{poT}} & \cdots & \mathbf{A}_{j}^{\mathrm{po} \rightarrow \mathrm{plT}} & \cdots & \mathbf{A}_{k}^{\mathrm{po} \rightarrow \mathrm{liT}} & \ldots \end{array}\right]^{\mathrm{T}} \\ \mathbf{b} &=\left[\begin{array}{lllll} \mathbf{b}_{i}^{\mathrm{po} \rightarrow \mathrm{poT}} & \cdots & \mathbf{b}_{j}^{\mathrm{po} \rightarrow \mathrm{plT}} & \cdots & \mathbf{b}_{k}^{\mathrm{po} \rightarrow {liT}} & \ldots \end{array}\right]^{\mathrm{T}} \end{aligned}\\ \begin{array}{l} \mathbf{A}_{i}^{\mathrm{po} \rightarrow \mathrm{po}}=\left[\begin{array}{l} \left.\mathbf{I}_{3}\left[\mathbf{p}_{i}\right]_{\times}\right] \quad \mathbf{b}_{i}^{\mathrm{po} \rightarrow \mathrm{po}}=\mathbf{q}_{i}-\mathbf{p}_{i} \end{array}\right.\\ \mathbf{A}_{j}^{\mathrm{po} \rightarrow \mathrm{pl}}=\left[\begin{array}{ll} \mathbf{n}_{j}^{T} & \left.\left(\mathbf{p}_{j} \times \mathbf{n}_{j}\right)^{\mathrm{T}}\right] & {\mathbf{b}_{j}^{\mathrm{po} \rightarrow \mathrm{pl}}}=\mathbf{n}_{j}^{\top}\left(\mathbf{q}_{j}-\mathbf{p}_{j}\right) \end{array}\right.\\ \mathbf{A}_{k}^{\mathrm{po} \rightarrow \mathrm{li}}=\left[\left[\mathbf{v}_{k}\right]_{\times} \quad\left(\mathbf{v}_{k}^{\top} \mathbf{p}_{k}\right) \mathbf{I}_{3}-\mathbf{p}_{k} \mathbf{v}_{k}^{\top}\right] \quad \mathbf{b}_{k}^{\mathrm{po\rightarrow}}=\mathbf{v}_{k} \times\left(\mathbf{q}_{k}-\mathbf{p}_{k}\right) \end{array}\]最终,待求解向量的求解形式如下:
\[\begin{aligned} \hat{\xi} &=\underset{\xi}(\mathbf{A} \xi-\mathbf{b})^{\top} \mathbf{P}(\mathbf{A} \xi-\mathbf{b})=\left(\mathbf{A}^{\top} \mathbf{P A}\right)^{-1}\left(\mathbf{A}^{\top} \mathbf{P} \mathbf{b}\right) \\ &=\left(\sum_{i=1}^{n} \mathbf{A}_{i}^{\top} w_{i} \mathbf{A}_{\mathrm{i}}\right)^{-1} \sum_{i=1}^{n} \mathbf{A}_{i}^{\top} w_{i} \mathbf{b}_{i} \end{aligned}\]第五步其实和第四步没有先后关系,是做的多策略的权重公式,文章中提出了基于残差、平衡方向贡献和强度一致性的多策略加权函数,形式如下:
\[w_{i}=w_{i}^{(\text {residual })} \times w_{i}^{\text {(balanced) }} \times w_{i}^{\text {(intensity) }}\\ w_{i}^{(\text {residual })}=\left\{\begin{array}{ll} 1, & \text { if } \kappa=2 \\ \frac{2 \epsilon_{i}}{\epsilon_{i}^{2}+2}, & \text { if } \kappa=0 \\ \epsilon_{i}\left(\frac{\epsilon_{i}^{2}}{|\kappa-2|}+1\right)^{\frac{\kappa}{2}-1}, & \text { otherwise } \end{array}\right.\\ w_{i}^{\text {(balanced) }}=\left\{\begin{array}{ll} \frac{|\mathcal{F}|+2|\mathcal{P}|-|\mathcal{B}|}{2(|\mathcal{G}|+|\mathcal{R}|)}, \quad i \in \mathcal{G} \text { or } i \in \mathcal{R} \\ 1, & \text { otherwise } \end{array}\right.\\ w_{i}^{(\text {intensity) }}=e^{-\frac{\mid \Delta I_{i}}{I_{\max }}}\]第六步是在ICP注册点云之后,评价注册质量,评价公式如下:
\[\hat{\sigma}^{2}=\frac{1}{n-6}(\mathbf{A} \hat{\xi}-\mathbf{b})^{\top} \mathbf{P}(\mathbf{A} \hat{\xi}-\mathbf{b}), \mathcal{I}=\frac{1}{\hat{\sigma}^{2}}\left(\mathbf{A}^{\top} \mathbf{P} \mathbf{A}\right)\]第七步是回环, 周期性保存的子图为处理单元, 子图之间的相邻和闭环边由 TEASER 全局注册构建和验证, 它的初始对应关系是根据顶点关键点的编码的 NCC 特征的余弦相似度确定的,以 TEASER 的估计作为初始猜测,map-to-map MULLS-ICP 用于通过精确的变换和信息矩阵来优化子图间边缘。那些 ˆσ 或 Ots 高于阈值的边将被删除,一旦添加了回环边,启动位姿图优化。
整体前后段流程总结为下图:
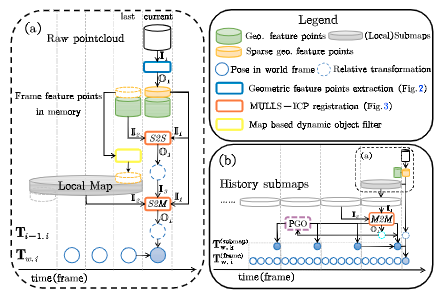
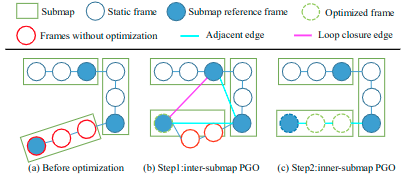
- 实验结果
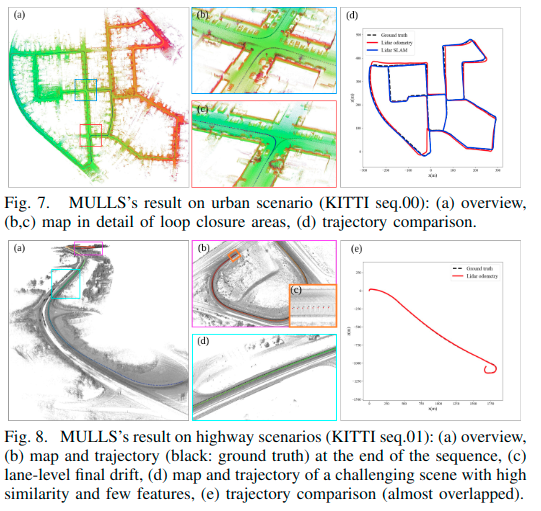
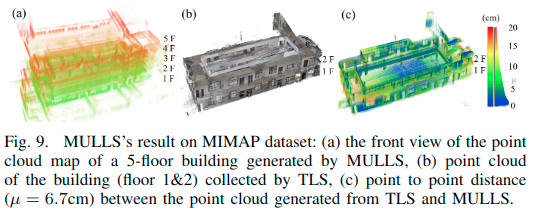
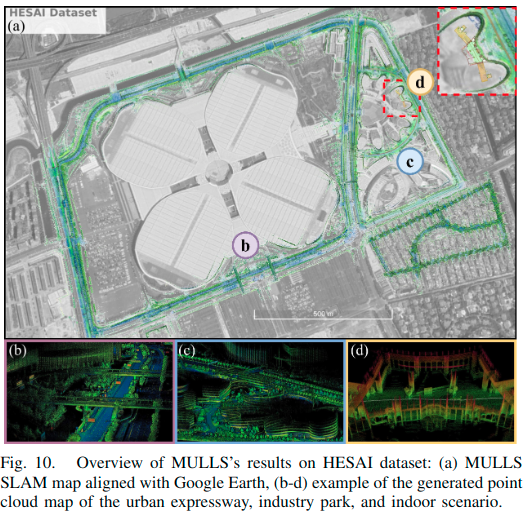
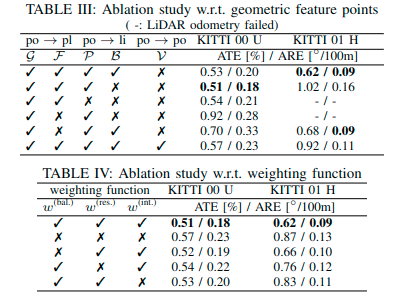
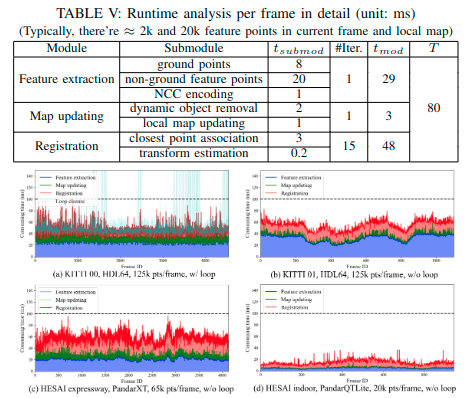
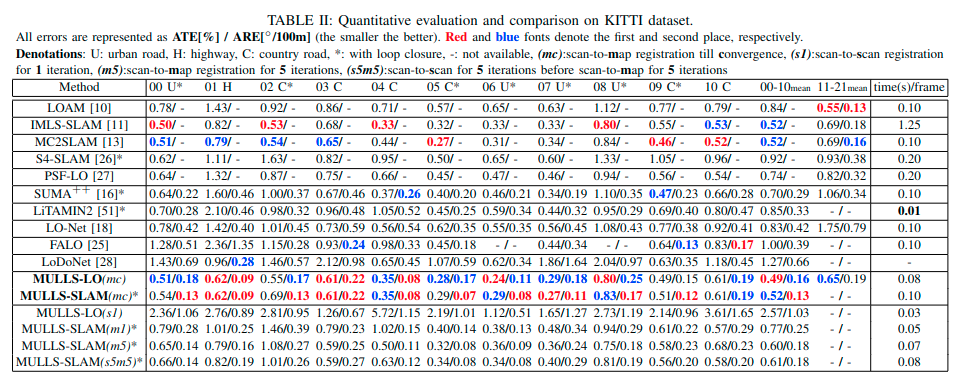
## Conclusion
这篇文章通过更细致的划分点云,将点云分成6类,然后分别对应着三种残差,不同残差根据不同点云的表现具有不同的权重,形成了一个比较有效的多重残差尺度的优化,后段回环论文中没有详细描述,不过从最终的实验结果来看也是很好的,并且因为对点云的细致分类,所以优化所需的时间比以前总体优化更快一点。
总的来说,这是一份非常不错的工作。
