论文阅读《CT-ICP: Real-time Elastic LiDAR Odometry with Loop Closure》

2021-10-23

KITTI榜单第六名的方法

论文54图片1

《CT-ICP: Real-time Elastic LiDAR Odometry with Loop Closure》(arxiv.2109.12979 )

Motivation

出发点主要是考虑到，一是匀速运动模型矫正点云畸变的做法无法适应大方向或者剧烈速度变化的情况，二是虽然目前有工作考虑了连续时间内的运动，建模了速度，但是也无法适应高频的剧烈运动情况。为了让里程计既能考虑单帧内的连续运动和连续帧的高频运动，作者提出了本篇的弹性里程计。

如下图:彩色点云表示一次 LiDAR 扫描；颜色取决于每个点的时间戳（从最旧的蓝色到最新的红色）。通过在扫描开始和结束时联合优化两个姿势并根据时间戳进行插值，使点云弹性变形与地图点云（白点）对齐，从而创建连续时间的帧到地图里程计。最下行的图代表轨迹具有扫描内姿势的连续性和扫描之间的不连续性。

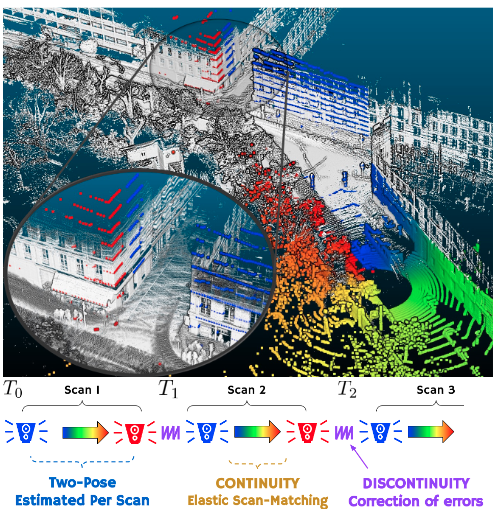
论文54图片2

Contribution

  1. 提出了一个具有扫描内姿态连续性和扫描间不连续性的新型弹性激光雷达里程计
  2. 基于稀疏体素结构中存储的密集点云的局部地图，以获得实时处理速度。
  3. 大量的实验以及开源的代码。
  4. 一种与位姿图后端集成的快速循环检测方法，目前已开源集成到 pyLiDAR-SLAM 中

Content

  1. 里程计公式构建

    在每一帧，里程计具有两个位姿，分别是帧起始位姿和帧结束位姿, 时间也一样:

\[\mathbf{X}=\left(\boldsymbol{\Omega}_{\boldsymbol{b}}, \boldsymbol{\Omega}_{\boldsymbol{e}}\right) \in S E(3)^{2}\\ \Omega_{b}^{n}=\left(R_{b}^{n}, t_{b}^{n}\right)\\ \Omega_{e}^{n}=\left(R_{e}^{n}, t_{e}^{n}\right)\\ \text { time } \tau \in\left[\tau_{b}, \tau_{e}\right]\]

与其他里程计不同的是，当前帧的起始位姿不等于上一帧的结束位姿，这两个位姿之间还存在一个邻近约束。

定义求解问题如下:

\[\underset{\mathbf{X} \in S E(3)^{2}} F_{\mathrm{ICP}}(\mathbf{X})+\beta_{l} C_(\mathbf{X})+\beta_{v} C_{\mathrm{vel}}(\mathbf{X})\\ F_{\mathrm{ICP}}(\mathbf{X})=\frac{1}{\left|\mathbb{I}^{n}\right|} \sum_{i \in \mathbb{I}^{n}} \rho\left(r_{i}^{2}[\mathbf{X}]\right)\\ \begin{aligned} r_{i}[\mathbf{X}] &=a_{i}\left(p_{i}^{W}[\mathbf{X}]-q_{i}^{W}\right) \cdot n_{i} (点面距离误差)\\ p_{i}^{W}[\mathbf{X}] &=R^{\alpha_{i}}[\mathbf{X}] * p_{i}^{L}+t^{\alpha_{i}}[\mathbf{X}] \\ R^{\alpha_{i}}[\mathbf{X}] &={slerp}\left(\mathbf{R}_{\mathbf{b}}, \mathbf{R}_{\mathbf{e}}, \alpha_{i}\right) \\ t^{\alpha_{i}}[\mathbf{X}] &=\left(1-\alpha_{i}\right) \mathbf{t}_{\mathbf{b}}+\alpha_{i} \mathbf{t}_{\mathbf{e}}\\ \end{aligned}\\ a_{i}=a_{2 D}=\left(\sigma_{2}-\sigma_{3}\right) / \sigma_{1}(点面距离误差的权重，引用自论文IMLS-SLAM,可以理解为邻居的平面度)\\ \begin{aligned} C_{l o c}\left(\mathbf{t}_{\mathbf{b}}\right) &=\left\|\mathbf{t}_{\mathbf{b}}-t_{e}^{n-1}\right\|^{2}(位置一致性约束) \\ C_{v e l}\left(\mathbf{t}_{\mathbf{b}}, \mathbf{t}_{\mathbf{e}}\right) &=\left\|\left(\mathbf{t}_{\mathbf{e}}-\mathbf{t}_{\mathbf{b}}\right)-\left(t_{e}^{n-1}-t_{b}^{n-1}\right)\right\|^{2}(匀速运动约束) \end{aligned}\\ \beta_{l} =\beta_{v}=0.001(实验参数)\]

  1. 局部地图和鲁棒的配置文件

    这部分论文里写的有点像是实验报告，两段话，大致讲了体素格参数配置和雷达点云帧插入标准的大致准则(判断角度变化是否大于阈值)。

  2. 回环检测和后段

    思路和SC有点类似，但是实现方式不一样

    将地图中的每个点插入到2D高程网格，使每个像素点保持在最大高度，在2D网格中，通过Zmin和Zmax的差值获取高程图像，然后提取旋转不变的2D特征并且和高程网格一起保存。提取到匹配对后，通过ICP和RANSAC约束位姿…

    总体而言，限制很多，首先要求是运动尽量是平面运动，然后要求将Z轴和地平面法向量对齐，这个回环不如用SC来代替。

  3. 实验结果

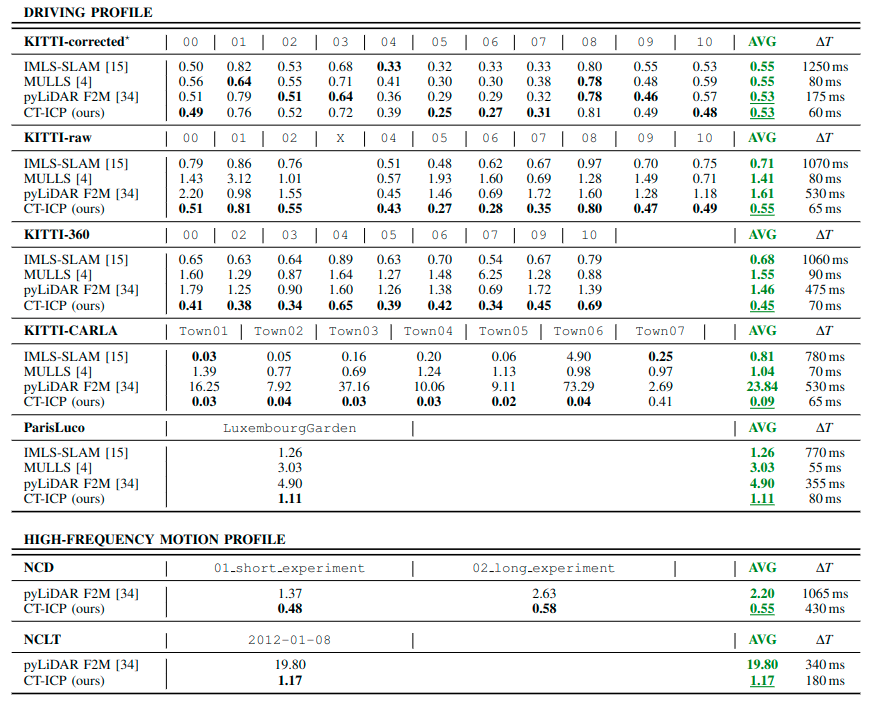
论文54图片3

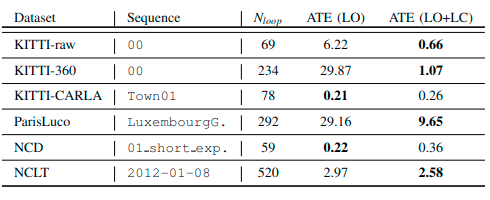
论文54图片4

Conclusion

这篇文章的作者和IMLS(18年ICRA)的作者是同一个人，不过区别在于这篇文章目前开源了，但是IMLS至今仍未开源，整体来讲，论文写的很粗糙，给我的感觉就是在IMLS的基础上，建模帧内和帧间约束，后段回环虽然是自己写的，但是感觉不是很使用，约束很多，肯定是不如SC的。整个框架的创新点不是很大，总结起来是两点，一是建模帧间帧内约束，二是代码开源+实验效果(我个人怀疑这个效果可能并不如IMLS，是通过调参达到的)。