KITTI榜单第五名的方法

《Globally Consistent 3D LiDAR Mapping with GPU-accelerated GICP Matching Cost Factors》(RAL 2021 )

Motivation

出发点，一是因为基于位姿图的帧到帧的局部里程计虽然可以达到实时性能，但是有时候会陷入局部最小值，并且位姿图的协方差难以定义；二是因为基于全局匹配的方法虽然会有很好的性能，但是计算资源消耗过大，难以在CPU上实现实时性能。所以在这篇文章中，结合GPU的计算性能和全局匹配的精确度，提出了一个实时且全局一致的三维激光雷达建图方案。

Contribution

1. 提出了一个基于GPU加速残差因子计算的全局一致的三维建图框架，并且证明了全局图的计算残差函数的实时性是可以达到的，论文里自称是第一个实时的执行全局尺度扫描匹配的方法。
2. 提出了一个可以在GPU上执行的基于重复程度的建图管理机制，并且可以执行通用的建图过程。
3. 证明了全局匹配方法可以保持大地图的一致性并且增强地图的质量。

Content

1. 系统框架

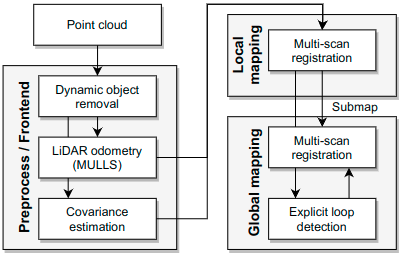
如上图，首先进行动态物体移除的工作(使用的RandLA-Net)，然后运行里程计算法(使用的是MULLS)获取最新的传感器位姿，并且从每个点的K近邻的点中估计它的协方差矩阵(因为最近邻搜索代价高昂，所以只在这个预处理步骤执行一次)。

然后预处理的点云和传感器位姿传输给局部建图模块(每个局部子图融合大约10-20帧)，并且在接下来的全局建图模块中，会将这些局部子图融合成全局图。建图模块的核心在于使用体素格化的GICP匹配因子构建因子图的多扫描匹配算法，如下图。在局部建图模块，构建一个全连接的因子图；在全局建图模块，在和最新子图有重叠部分的每一个子图之间都构建约束。

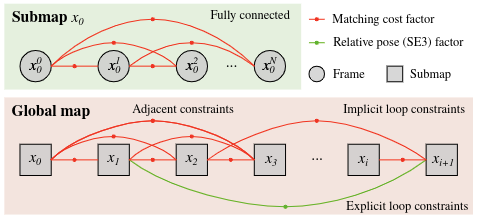
1. 体素格化的GICP匹配因子

   目标函数定义为如下:

\[f^{M}\left(\mathcal{F}^{M}, \mathcal{T}\right)=\sum_{(i, j) \in \mathcal{F} M} e^{M}\left(\mathcal{P}_{i}, \mathcal{P}_{j}, \boldsymbol{T}_{i}, \boldsymbol{T}_{j}\right)(e^M是匹配代价函数)\]

匹配代价函数被定义为VGICP(体素格化的GICP), GICP的误差形式如下:

\[e^{G I C P}\left(\boldsymbol{p}_{k}, \boldsymbol{T}\right)=\boldsymbol{d}_{k}^{T}\left(\boldsymbol{C}_{k}^{\prime}+\boldsymbol{T} \boldsymbol{C}_{k} \boldsymbol{T}^{T}\right)^{-1} \boldsymbol{d}_{k}\\ p_k是协方差:p_k=(\mu_k,C_k)\\ d_k=\mu'_k-T\mu_k\]

原始的GICP的匹配点对是通过KD-Tree进行搜索，但是KD-Tree并不适合GPU,因为KD-Tree中有很多条件分支。所以为了最大化利用GPU，采用基于体素格的数据关联方式，VGICP将点的分布聚合成体素格的分布(这个和NDT方法不同，NDT是从点集中计算体素格的分布); 这种方法仅用几个点就可以获得体素格上的有效分布，并且具有更强的鲁棒性和精确度相比较于NDT。

结合上面两个公式，获得匹配残差的新的表示形式:

\[e^{M}\left(\mathcal{P}_{i}, \mathcal{P}_{j}, \boldsymbol{T}_{i}, \boldsymbol{T}_{j}\right)=\sum_{\boldsymbol{p}_{k} \in \mathcal{P}_{i}} e^{G I C P}\left(\boldsymbol{p}_{k}, \boldsymbol{T}_{i j}\right)\]

求导获取海塞因子$H_ii,H_ij,H_jj 和系数向量b_i,b_j$约束相邻位姿:

\[\begin{aligned} \boldsymbol{A}_{k} &=\frac{\partial \boldsymbol{e}_{k}}{\partial \boldsymbol{T}_{i}}, \boldsymbol{B}_{k}=\frac{\partial \boldsymbol{e}_{k}}{\partial \boldsymbol{T}_{j}} \\ \boldsymbol{H}_{i i} &=\sum_{k}^{N} \boldsymbol{A}_{k}^{T} \boldsymbol{\Omega}_{k} \boldsymbol{A}_{k}, \boldsymbol{H}_{i j}=\sum_{k}^{N} \boldsymbol{A}_{k}^{T} \boldsymbol{\Omega}_{k} \boldsymbol{B}_{k}, \\ \boldsymbol{H}_{j j} &=\sum_{k}^{N} \boldsymbol{B}_{k}^{T} \boldsymbol{\Omega}_{k} \boldsymbol{B}_{k}, \\ \boldsymbol{b}_{i} &=\sum_{k}^{N} \boldsymbol{A}_{k}^{T} \boldsymbol{\Omega}_{k} \boldsymbol{e}_{k}, \boldsymbol{b}_{j}=\sum_{k}^{N} \boldsymbol{B}_{k}^{T} \boldsymbol{\Omega}_{k} \boldsymbol{e}_{k} \end{aligned}\\ e_k=\mu'_k-T_{ij}\mu_k\\ \Omega_k=C'_k+T_{ij}C_kT^T_{ij}\]

1. 局部建图

   局部建图模块的目的是通过把大量的连续帧合并到一个局部子图来减少全局建图模块的所需要优化位姿的数量。

   管理建图模块的标准是基于简单细粒度的重叠标准，重叠标准的定义是A点云中的点在B点云中的数量除以A点云的数量:

\[\begin{aligned} s\left(\boldsymbol{p}_{\boldsymbol{k}}, \mathcal{P}_{j}\right) &=\left\{\begin{array}{ll} 1 & \text { if } \boldsymbol{p}_{k} \text { fell in a voxel of } \mathcal{P}_{j} \\ 0 & \text { otherwise } \end{array}\right.\\ \operatorname{overlap}\left(\mathcal{P}_{i}, \mathcal{P}_{j}\right) &=\frac{\sum_{k}^{N} s\left(\boldsymbol{p}_{k}, \mathcal{P}_{j}\right)}{N} \end{aligned}\]

然后如果新的点云帧的重复度大于阈值，则跳过，小于阈值则体素格化后插入当前局部子图的因字图，并且为新插入的帧和当前子图中拥有的所有帧都构建因子，因此是个全连接；然后，当第一帧和最后一帧的重叠度低于一定阈值的时候则执行因子图优化，然后把这个局部子图送到全局建图模块。

1. 全局建图模块

   全局建图模块将因子图优化后的局部子图作为输入，输出的是对齐后的全部图。

   相比较于传统的扫描匹配建图方式，文中提出的集于子图的匹配代价因子可以计算出两个很相似帧的相对位姿，如下图:

但是因为匹配代价因子使用的是集于体素格的数据关联方式，当估计漂移很大的时候，它可能会陷入局部解, 如下图:

为了解决这种情况，就需要引入外部的回环检测作为约束, 因此全局建图的目标函数最终定义如下:

\[\begin{aligned} f^{G}(\mathcal{T}) &=f^{M}\left(\mathcal{F}_{G}^{M}, \mathcal{T}\right)+f^{L}\left(\mathcal{F}_{G}^{L}, \mathcal{T}\right) \\ f^{L}\left(\mathcal{F}^{L}, \mathcal{T}\right) &=\sum_{(i, j) \in \mathcal{F}^{L}} \rho\left(\left\|\log \left(\hat{\boldsymbol{T}}_{i j}^{-1} \boldsymbol{T}_{i}^{-1} \boldsymbol{T}_{j}\right)\right\|^{2}\right) \end{aligned}\]

引入回环检测后，对比图如下:

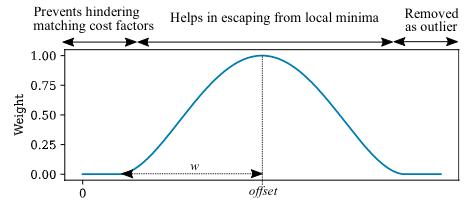
并且为了充分利用回环的匹配条件，加入一个Tukey鲁棒核函数:

\[\begin{aligned} \operatorname{tukey}(x, w) &=\max \left(0,\left(1-x^{2} / w\right)^{2}\right) \\ \text { shiftedtukey }(x, w, offset ) &=\operatorname{tukey}(\|x-o f f \operatorname{set}\|, w) \end{aligned}\]

如下图:这核函数强制优化以满足循环约束，同时避免在相对位姿误差较小时破坏匹配。核函数还删除了错误的闭环因为异常值太大。

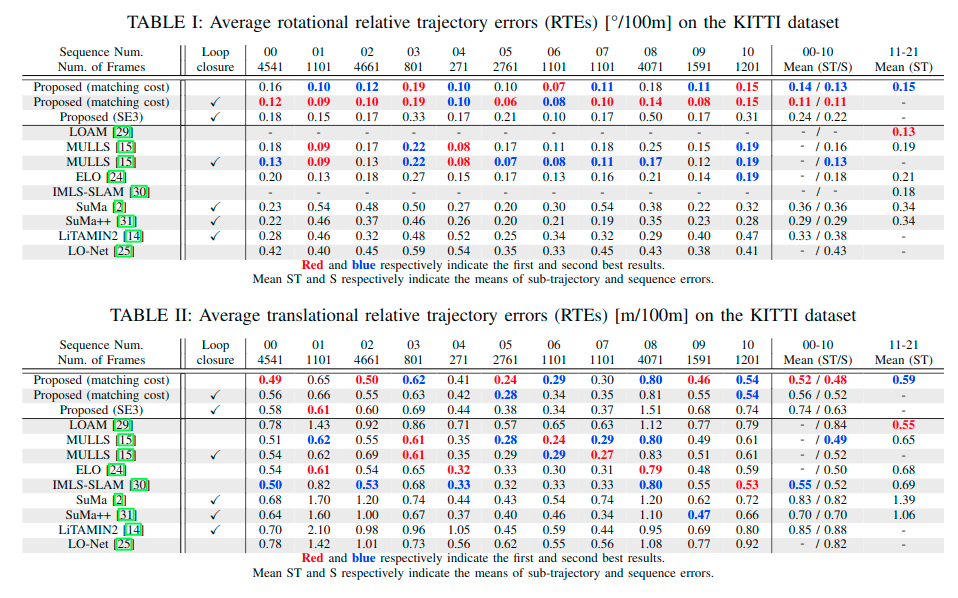
1. 实验结果

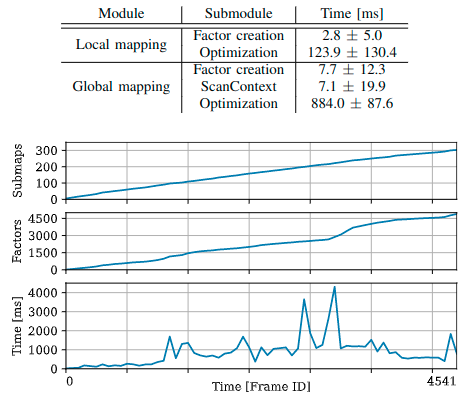
Conclusion

这篇文章主要做的工作是将VGICP移植到GPU上，实现了全局匹配的实时性能，VGICP目前我尚未接触过，但是看文章中的描述是和NDT有点类似的，后续有空可以研究下。