R2live的进阶版本,从视频看,效果比R2live好了很多,无论是精度还是可视化的效果,另外github中给出的VR的应用也挺有意思。
《R3LIVE: A Robust, Real-time, RGB-colored, LiDAR-Inertial-Visual tightly-coupled state Estimation and mapping package》(arXiv:2109.07982, 就这个视频效果而言,中ICRA2022是保底的 )
Motivation
基于R2LIVE延伸,从视频中可以看出,作者是想要提升鲁棒性,具体场景是窄视角的激光雷达在狭窄通道的情况(视频中极端的将雷达对准周围墙壁,可以理解为雷达完全失效)。
Contribution
-
提出了一个融合框架,包含定位建图和上色,框架里包含一个LIO模块和一个VIO模块,整个系统可以实时的重建密集3D彩色环境。
-
基于彩色RGB点云提出了一个新的VIO系统,通过最小化三维地图点颜色和该三维点在当前图像帧中的颜色的光度误差,避免了提取突出的视觉特征点的需求,提升了运行速度,并且使得这个VIO对于无纹理环境更加鲁棒。
-
丰富的实验和开源的代码
Content
-
系统框架
包含两个子系统:VIO和LIO, LIO主要用来构建全局地图和估计系统状态,VIO用来更新地图的纹理和更新系统状态。
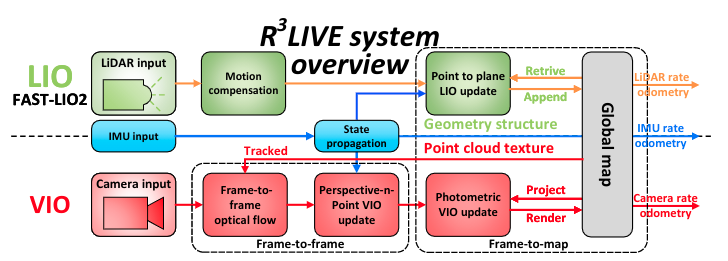
-
LIO
用的直接是Fast-Lio, 简单地说用IMU补偿运动,然后用ESIKF最小化点面误差更新位姿,最终构建地图。
-
VIO
这部分是本篇论文的重点,将VIO分成了两步,一是直接通过帧间的光流来追踪地图点,并且通过最小化追踪到的地图点的PNP投影误差来获取系统状态;二是通过这些地图点的出现的帧到地图的光度误差来优化状态
A. 帧到帧的VIO
首先将三维地图点投影到上一个图像帧获取二维座标然后通过LK光流法获取到在当前帧的二维坐标,然后可以通过ESIKF计算误差更新状态(计算PNP,更新ESIKF):
ESIKF更新VIO是通过最小化PNP误差更新的,示意图如下:
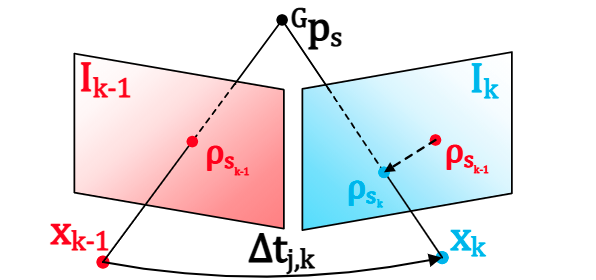
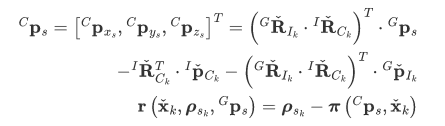
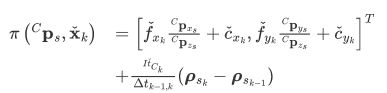
测量噪声包含两个来源,一个是像素追踪误差,另一个是地图点定位误差:
\[\begin{aligned} { }^{G} \mathbf{p}_{s} &={ }^{G} \mathbf{p}_{s}^{\mathrm{gt}}+\mathbf{n}_{\mathbf{p}_{s}}, \mathbf{n}_{\mathbf{p}_{s}} \sim \mathcal{N}\left(\mathbf{0}, \boldsymbol{\Sigma}_{\mathbf{n}_{\mathbf{p}_{s}}}\right) \\ \boldsymbol{\rho}_{s_{k}} &=\boldsymbol{\rho}_{s_{k}}^{\mathrm{gt}}+\mathbf{n}_{\boldsymbol{\rho}_{s_{k}}}, \mathbf{n}_{\boldsymbol{\rho}_{s_{k}}} \sim \mathcal{N}\left(\mathbf{0}, \boldsymbol{\Sigma}_{\mathbf{n}_{\boldsymbol{\rho}_{k_{k}}}}\right) \end{aligned}\]然后将残差一阶泰勒展开:
\[\mathbf{0}=\mathbf{r}\left(\mathbf{x}_{k}, \boldsymbol{\rho}_{s_{k}}^{\mathrm{gt}},{ }^{G} \mathbf{p}_{s}^{\mathrm{gt}}\right) \approx \mathbf{r}\left(\check{\mathbf{x}}_{k}, \boldsymbol{\rho}_{s_{k}},{ }^{G} \mathbf{p}_{s}\right)+\mathbf{H}_{s}^{r} \delta \check{\mathbf{x}}_{k}+\boldsymbol{\alpha}_{s}\\ \begin{aligned} \mathbf{H}_{s}^{r} &=\left.\frac{\partial \mathbf{r}_{c}\left(\check{\mathbf{x}}_{k} \oplus \delta \check{\mathbf{x}}_{k}, \boldsymbol{\rho}_{s_{k}},{ }^{G} \mathbf{p}_{s}\right)}{\partial \delta \check{\mathbf{x}}_{k}}\right|_{\delta \check{\mathbf{x}}_{k}=\mathbf{0}} \\ \boldsymbol{\Sigma}_{\boldsymbol{\alpha}_{s}} &=\boldsymbol{\Sigma}_{\mathbf{n}_{\boldsymbol{s}_{s_{k}}}}+\mathbf{F}_{\mathbf{p}_{s}}^{r} \boldsymbol{\Sigma}_{\mathbf{p}_{s}} \mathbf{F}_{\mathbf{p}_{s}}^{r} T \\ \mathbf{F}_{\mathbf{p}_{s}}^{r} &=\frac{\partial \mathbf{r}\left(\check{\mathbf{x}}_{k}, \boldsymbol{\rho}_{s_{k}},{ }^{G} \mathbf{p}_{s}\right)}{\partial^{G} \mathbf{p}_{s}} \end{aligned}\\ \boldsymbol{\alpha}_{s} \sim \mathcal{N}\left(\mathbf{0}, \boldsymbol{\Sigma}_{\boldsymbol{\alpha}_{s}}\right)\]根据这个一阶展开,可以和IMU传播的先验分布组合,获得当前估计位姿的MAP:
\[\begin{array}{l} \min _{\delta \dot{\mathbf{x}}_{k}}\left(\left\|\check{\mathbf{x}}_{k} \ominus \hat{\mathbf{x}}_{k}+\mathcal{H} \delta \check{\mathbf{x}}_{k}\right\|_{\boldsymbol{\Sigma}_{\delta \tilde{\mathbf{x}}_{k}}}^{2}\right. \\ \left.\quad+\sum_{s=1}^{m}\left\|\mathbf{r}\left(\check{\mathbf{x}}_{k}, \boldsymbol{\rho}_{s_{k}},{ }^{G} \mathbf{p}_{s}\right)+\mathbf{H}_{s}^{r} \delta \check{\mathbf{x}}_{k}\right\|_{\boldsymbol{\Sigma}_{\boldsymbol{\alpha}_{s}}}^{2}\right) \end{array}\]给出卡尔曼滤波的相关定义:
\[\begin{aligned} \mathbf{H} &=\left[\mathbf{H}_{1}^{r T}, \ldots, \mathbf{H}_{m}^{r}\right]^{T} \\ \mathbf{R} &=\operatorname{diag}\left(\boldsymbol{\Sigma}_{\boldsymbol{\alpha}_{1}}, \ldots, \boldsymbol{\Sigma}_{\boldsymbol{\alpha}_{m}}\right) \\ \check{\mathbf{z}}_{k} &=\left[\mathbf{r}\left(\check{\mathbf{x}}_{k}, \boldsymbol{\rho}_{1_{k}},{ }^{G} \mathbf{p}_{1}\right) \ldots, \mathbf{r}\left(\check{\mathbf{x}}_{k}, \boldsymbol{\rho}_{m_{k}},{ }^{G} \mathbf{p}_{m}\right)\right]^{T} \\ \mathbf{P} &=(\mathcal{H})^{-1} \boldsymbol{\Sigma}_{\delta \hat{\mathbf{x}}_{k}}(\mathcal{H})^{-T} \end{aligned}\]卡尔曼增益可以定义为:
\[\mathbf{K}=\left(\mathbf{H}^{T} \mathbf{R}^{-1} \mathbf{H}+\mathbf{P}^{-1}\right)^{-1} \mathbf{H}^{T} \mathbf{R}^{-1}\]状态更新为:
\[\check{\mathbf{x}}_{k}=\check{\mathbf{x}}_{k} \oplus\left(-\mathbf{K} \check{\mathbf{z}}_{k}-(\mathbf{I}-\mathbf{K H})(\mathcal{H})^{-1}\left(\check{\mathbf{x}}_{k} \ominus \hat{\mathbf{x}}_{k}\right)\right)\]并且根据Fast-lio的公式推导,这样的迭代更新过程是等价于高斯牛顿优化的。
B. 帧到地图的VIO
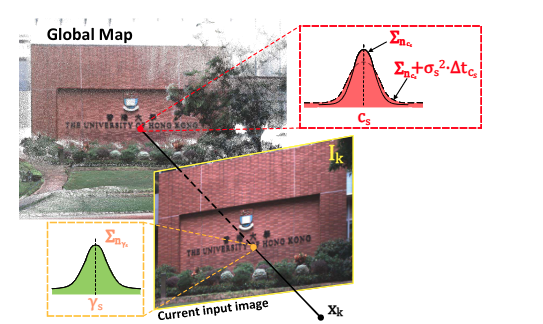
基本上和帧到帧的VIO一样:
误差直接用帧到三维地图点的光度误差:
\[\mathbf{o}\left(\check{\mathbf{x}}_{k},{ }^{G} \mathbf{p}_{s}, \mathbf{c}_{s}\right)=\mathbf{c}_{s}-\gamma_{s}\]两个参数有各自对应的测量噪声:
\[\begin{array}{r} \gamma_{s}=\boldsymbol{\gamma}_{s}^{g t}+\mathbf{n}_{\boldsymbol{\gamma}_{s}}, \mathbf{n}_{\boldsymbol{\gamma}_{s}} \sim \mathcal{N}\left(\mathbf{0}, \boldsymbol{\Sigma}_{\mathbf{n}_{\gamma_{s}}}\right) \\ \mathbf{c}_{s}=\mathbf{c}_{s}^{g t}+\mathbf{n}_{\mathbf{c}_{s}}+\boldsymbol{\eta}_{\mathbf{c}_{s}}, \mathbf{n}_{\mathbf{c}_{s}} \sim \mathcal{N}\left(\mathbf{0}, \boldsymbol{\Sigma}_{\mathbf{n}_{\mathrm{c}_{s}}}\right) \\ \eta_{\mathbf{c}_{s}} \sim \mathcal{N}\left(\mathbf{0}, \boldsymbol{\sigma}_{s}^{2} \cdot \Delta t_{\mathbf{c}_{s}}\right) \end{array}\]一阶泰勒展开:
\[\mathbf{0}=\mathbf{o}\left(\mathbf{x}_{k},{ }^{G} \mathbf{p}_{s}^{g t}, \mathbf{c}_{s}^{g t}\right) \approx \mathbf{o}\left(\check{\mathbf{x}}_{k},{ }^{G} \mathbf{p}_{s}, \mathbf{c}_{s}\right)+\mathbf{H}_{s}^{o} \delta \check{\mathbf{x}}_{k}+\boldsymbol{\beta}_{s}\\ \begin{array}{l} \mathbf{H}_{s}^{o}=\left.\frac{\partial \mathbf{o}\left(\check{\mathbf{x}}_{k} \text { 田 } \delta{\mathbf{x}}_{k},{ }^{G} \mathbf{p}_{s}, \mathbf{c}_{s}\right)}{\partial \delta \check{\mathbf{x}}_{k}}\right|_{\delta \tilde{\mathbf{x}}_{k}=0} \\ \boldsymbol{\Sigma}_{\boldsymbol{\beta}_{s}}=\boldsymbol{\Sigma}_{\mathbf{n}_{\mathrm{c}_{s}}}+\boldsymbol{\sigma}_{s}^{2} \cdot \Delta t_{\mathbf{c}_{s}}+\boldsymbol{\Sigma}_{\mathbf{n}_{\gamma_{s}}}+\mathbf{F}_{\mathbf{p}_{s}}^{o} \boldsymbol{\Sigma}_{\mathbf{p}_{s}} \mathbf{F}_{\mathbf{p}_{s}}^{o T} \\ \mathbf{F}_{\mathbf{p}_{s}}^{o}=\frac{\partial \mathbf{o}\left(\check{\mathbf{x}}_{k},{ }^{G} \mathbf{p}_{s}, \mathbf{c}_{s}\right)}{\partial^{G} \mathbf{p}_{s}} \end{array}\\ \boldsymbol{\beta}_{s} \sim \mathcal{N}\left(\mathbf{0}, \boldsymbol{\Sigma}_{\beta_{s}}\right)\]构建MAP问题:
\[\begin{array}{l} \min _{\delta \tilde{\mathbf{x}}_{k}}\left(\left\|\check{\mathbf{x}}_{k} \ominus \hat{\mathbf{x}}_{k}+\mathcal{H} \delta \check{\mathbf{x}}_{k}\right\|_{\boldsymbol{\Sigma}_{\delta \hat{\mathbf{x}}_{k}}}^{2}\right. \\ \left.\quad+\sum_{s=1}^{m}\left\|\mathbf{o}\left(\check{\mathbf{x}}_{k},{ }^{G} \mathbf{p}_{s}, \mathbf{c}_{s}\right)+\mathbf{H}_{s}^{o} \delta{\mathbf{x}}_{k}\right\|_{\boldsymbol{\Sigma}_{\boldsymbol{\beta}_{s}}}^{2}\right) \end{array}\]卡尔曼定义,增益,及更新:
\[\begin{aligned} \mathbf{H} &=\left[\mathbf{H}_{1}^{o T}, \ldots, \mathbf{H}_{m}^{oT}\right]^{T} \\ \mathbf{R} &=\operatorname{diag}\left(\boldsymbol{\Sigma}_{\boldsymbol{\beta}_{1}}, \ldots, \boldsymbol{\Sigma}_{\boldsymbol{\beta}_{m}}\right) \\ \check{\mathbf{z}}_{k} &=\left[\mathbf{o}\left(\check{\mathbf{x}}_{k},{ }^{G} \mathbf{p}_{1}, \mathbf{c}_{1}\right) \ldots, \mathbf{o}\left(\check{\mathbf{x}}_{k},{ }^{G} \mathbf{p}_{m}, \mathbf{c}_{m}\right)\right]^{T} \\ \mathbf{P} &=(\mathcal{H})^{-1} \boldsymbol{\Sigma}_{\delta \hat{\mathbf{x}}_{k}}(\mathcal{H})^{-T} \end{aligned}\] \[\hat{\mathbf{x}}_{k}=\check{\mathbf{x}}_{k}, \quad \boldsymbol{\Sigma}_{\delta \hat{\mathbf{x}}_{k}}=(\mathbf{I}-\mathbf{K H}) \boldsymbol{\Sigma}_{\delta \tilde{\mathbf{x}}_{k}}\]C. 渲染全局地图的纹理
这个环节紧接着帧到地图的VIO,总的来讲就是对当前地图帧的活跃的voxel根据图像帧上色,然后再进行线形插值平滑色彩,最后根据地图点的色彩和观察的色彩进行贝叶斯更新:
\[\begin{array}{r} \boldsymbol{\Sigma}_{\mathbf{n}_{\tilde{c}_{s}}}=\left(\left(\boldsymbol{\Sigma}_{\mathbf{n}_{\mathbf{c}_{s}}}+\boldsymbol{\sigma}_{s}^{2} \cdot \Delta t_{\mathbf{c}_{s}}\right)^{-1}+\boldsymbol{\Sigma}_{\mathbf{n}_{\gamma_{s}}}^{-1}\right)^{-1} \\ \tilde{\mathbf{c}}_{s}=\left(\left(\boldsymbol{\Sigma}_{\mathbf{n}_{\mathrm{c}_{s}}}+\boldsymbol{\sigma}_{s}^{2} \cdot \Delta t_{\mathbf{c}_{s}}\right)^{-1} \mathbf{c}_{s}+\boldsymbol{\Sigma}_{\mathbf{n}_{\gamma_{s}}}^{-1} \gamma_{s}\right)^{-1} \boldsymbol{\Sigma}_{\mathbf{n}_{\tilde{c}_{s}}} \\ \mathbf{c}_{s}=\tilde{\mathbf{c}}_{s}, \quad \boldsymbol{\Sigma}_{\mathbf{n}_{\mathrm{c}_{s}}}=\boldsymbol{\Sigma}_{\mathbf{n}_{\tilde{c}_{s}}} \end{array}\]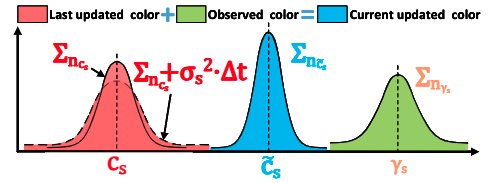
D. 更新VIO中的跟踪点
排除两类点,一是PNP误差或者光度误差过大的点,二是排除像素坐标不在当前图像帧的点。
将地图点投影到图像帧,如果一个像素周围没有地图点,则把他三维化后加入到地图。
- 实验
建议直接看作者的油管,可视化的实验效果很好, 这个文章是作者的初稿,所以数据肯定还没整理好。
A. 鲁棒性实验(激光退化,视觉无纹理)
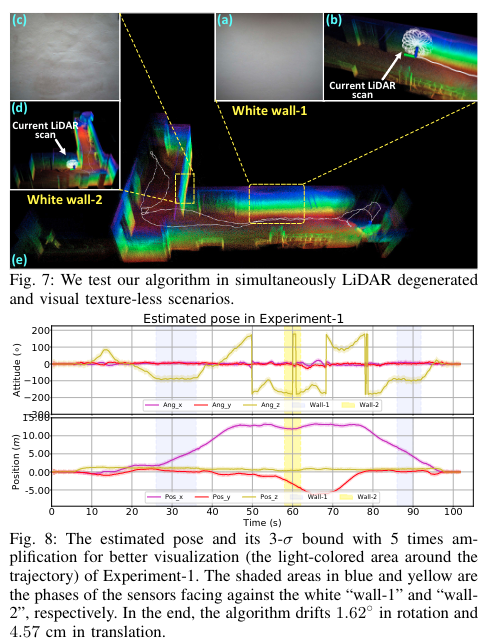
B. 大规模的高精度建图


C. 量化结果
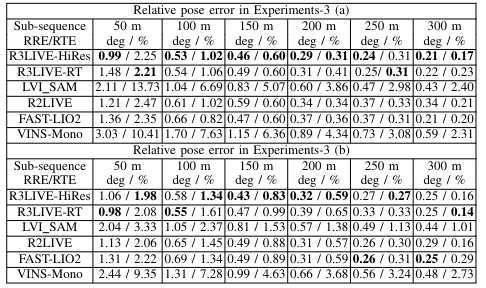
D. 时间消耗

E. 网格重建

F. 模拟应用

G. AR游戏

Conclusion
R3live这个工作相比于R2live, 继承的是分lio和vio模块化处理的思想,仍然是都没有采用联合优化,进步的是地图方面的构建和VIO的ESIKF过程,从视频效果来看,可以完美的处理长廊问题,是一个非常好的工作。
