《GR-SLAM: Vision-Based Sensor Fusion SLAM for Ground Robots on Complex Terrain》(IROS2020)
Motivation
作者在实验中发现,大多数现有的VIO方法在无人机上表现不错,但是在复杂地形的地面机器人的定位上,效果比较差。虽然有一些工作基于平面运动的假设可以辅助修复定位,但是应用很受限。所以作者在这篇文章中提出了一个VIO+encoder融合的紧耦合方案来解决这个问题。
Contribution
1.提出了一种里程表增量模型,该模型可以融合编码器和IMU数据计算机器人位姿增量,以适应大型复杂地形的三维环境。
- 提出了一个完整的因子图优化框架,它可以紧密耦合摄像头、IMU和encoder数据,也可以检测异常数据并调整优化每个传感器的权重。
- 在基于真实地面机器人的大规模实验(室内和室外环境)表明GR-SLAM算法用于地面机器人的精度和鲁棒性。
Content
-
参数矫正
这个模块主要是解决encoder的内参和VIO的外参矫正问题,不作详细介绍,感兴趣的同学可以阅读原文。
-
系统框架
整体框架如下,包括四个线程,前端线程包括传感器数据同步和运动帧生成;轮式里程计矫正线程仅在第一次运动的时候启动,并且矫正参数在之后优化矫正后固定;核心线程是滑窗优化线程;最后有回环线程辅助矫正位姿
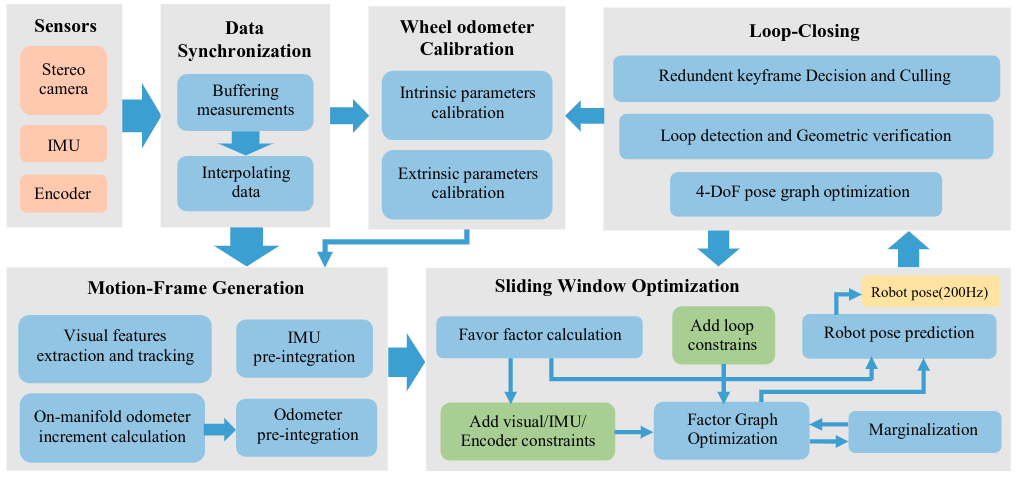
-
流型上的里程计增量模型
这个模型的提出,主要是适应复杂地形的大的梯度变化的情况,目前现有的方法都是基于绝对或者随机平面假设,这导致在梯度变化快的大的复杂3D环境中适应性很差。所以,作者采用将两个高频(200HZ)的轮式里程计和IMU结合,增量更新运动模型,示意图如下:
$C_{ij}$这个弧是移动轨迹, $L_{ij}$是运动向量,$d\theta_{pitch}$和$d\phi_{yaw}$分别是在$yaw$和$pitch$变化的角度。
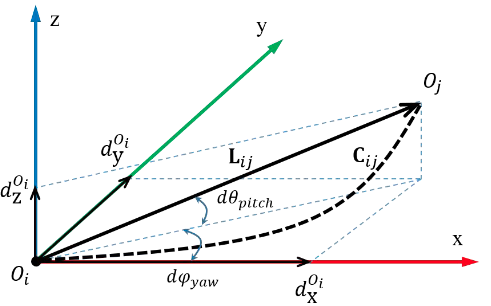
考虑到旋转一般在5ms内完成,那么长度可以近似为:
\[l_{ij}=c_{ij}\cos(d\phi_{yaw}/3)\]最后将运动向量投影到坐标轴上,可以得到三个运动增量:
\[d p_{o_{i} o_{j}}=\left[\begin{array}{l} c_{i j} \cos \left(d \varphi_{y a w} / 3\right) \cos \left(d \theta_{\text {pitch }}\right) \cos \left(d \varphi_{\text {yaw }}\right) \\ c_{i j} \cos \left(d \varphi_{\text {yaw }} / 3\right) \cos \left(d \theta_{\text {pitch }}\right) \sin \left(d \varphi_{\text {yaw }}\right) \\ -c_{i j} \cos \left(d \varphi_{\text {yaw }} / 3\right) \sin \left(d \theta_{\text {pich }}\right) \end{array}\right]\]-
传感器因子和动态权重
相机传感器因子采用的重投影误差:
通过预积分的方式构建IMU因子
\[\begin{array}{r} \mathbf{r}_{I}\left(\mathbf{z}_{I_{k} I_{k+1}}^{I}, \boldsymbol{\chi}\right)=\left[\begin{array}{l} \left.\delta \boldsymbol{\alpha}_{I_{k} I_{k+1}}^{I} \delta \boldsymbol{\beta}_{I_{k} I_{k+1}}^{I} \delta \boldsymbol{\theta}_{I_{k} I_{k+1}}^{I} \delta \mathbf{b}_{a} \delta \mathbf{b}_{g}\right]^{\mathrm{T}} \\ {\left[\mathbf{R}_{I_{k} w}\left(\mathbf{p}_{w I_{k+1}}-\mathbf{p}_{w I_{k}}+\frac{1}{2} \mathbf{g}_{w} \Delta t_{k}^{2}-\mathbf{v}_{w I_{k}} \Delta t_{k}\right)-\boldsymbol{\alpha}_{I_{k} I_{k+1}}^{I}\right.} \\ \mathbf{R}_{I_{k} w}\left(\mathbf{v}_{w I_{k+1}}+\mathbf{g}_{w} \Delta t_{k}-\mathbf{v}_{w I_{k}}\right)-\boldsymbol{\beta}_{I_{k} I_{k+1}}^{I} \\ 2\left[\left(\mathbf{q}_{w I_{k}}\right)^{-1} \otimes \mathbf{q}_{w I_{k+1}} \otimes\left(\boldsymbol{\theta}_{I_{k} I_{k+1}}^{I}\right)^{-1}\right]_{x y z} \\ \mathbf{b}_{a k+1}-\mathbf{b}_{a k} \\ \mathbf{b}_{g k+1}-\mathbf{b}_{g k} \end{array}\right. \end{array}\]根据上面描述的运动增量模型,可以对轮式里程计进行预积分构建因子,对于轮式里程计的预积分残差定义如下:
\[\begin{array}{l} \mathbf{r}_{O}\left(\mathbf{z}_{I_{k} I_{k+1}}^{O}, \boldsymbol{\chi}\right)=\left[\delta \boldsymbol{\alpha}_{I_{k} I_{k+1}}^{O} \delta \boldsymbol{\beta}_{I_{k} I_{k+1}}^{O}\right]^{\mathrm{T}} \\ =\left[\begin{array}{l} \mathbf{R}_{I_{k} w}\left(\mathbf{p}_{w I_{k+1}}-\mathbf{p}_{w I_{k}}\right)-\boldsymbol{\alpha}_{I_{k} I_{k+1}}^{O} \\ \mathbf{R}_{I_{k} w}\left(\mathbf{v}_{w I_{k+1}}-\mathbf{v}_{w I_{k}}\right)-\boldsymbol{\beta}_{I_{k} I_{k+1}}^{O} \end{array}\right] \end{array}\]传播用到了IMU预积分的误差($\eta$):
\[\left[\begin{array}{c} \delta \mathbf{p}_{k+1}^{i} \\ \delta \mathbf{v}_{k+1}^{i} \end{array}\right]=\left[\begin{array}{c} \delta \mathbf{p}_{k}^{i}+\mathbf{R}_{I_{k}}^{I_{i}} \mathbf{\eta}_{d}+\mathbf{R}_{I_{k}}^{I_{i}} \delta \mathbf{R}_{I_{k}}^{I_{i}} \mathbf{p}_{k}^{i} \\ \delta \mathbf{v}_{k}^{i}+\mathbf{R}_{I_{k}}^{I_{i}} \mathbf{\eta}_{v}+\mathbf{R}_{I_{k}}^{I_{i}} \delta \mathbf{R}_{I_{k}}^{I_{i}} \mathbf{v}_{k}^{i} \end{array}\right]\]三个因子的权重根据下面的公式进行更新:
\[\left\{\begin{array}{l} f_{p k}=\left(\frac{\left.\left\|\mathbf{p}_{t_{k} I_{k+1}}^{I}\right\|\right)}{\left\|\mathbf{p}_{t_{k} I_{k+1}}^{O}\right\|} \|^{2}, 0 \leq f_{p k} \leq 1\right. (帧起始位姿和帧结束位姿) \\ f_{r k}=\frac{\| \boldsymbol{\theta}_{I_{k} I_{k+1}}^{I}}{T_{\theta}}, 0 \leq f_{r k} \leq 0.5 (运动帧的位姿更新增量)\\ f_{c k}=\left(\frac{\left\|\mathbf{p}_{I_{k} I_{k+1}}^{C}\right\|-\| \mathbf{p}_{I_{k} I_{k+1}}^{I}}{\left\|\mathbf{p}_{I_{k} I_{k+1}}^{I}\right\|}\right)^{2}, 0 \leq f_{c k} \leq 1 (PNP位姿和帧起始位姿)\\ F_{k}^{O}=f_{p k}\left(1-f_{r k}\right), 0 \leq F_{k}^{O} \leq 1 (轮式里程计因子权重)\\ F_{k}^{I}=f_{r k}\left(1-f_{p k}\right), 0.5 \leq F_{k}^{I} \leq 1 (IMU因子权重)\\ F_{k}^{C}=1-f_{c k}, 0 \leq F_{k}^{C} \leq 1 (相机权重) \end{array}\right.\]最终的优化形式如下:
\[\begin{array}{l} \chi^{*}=\arg \min \left\{\left(\mathbf{H}_{p} \delta \boldsymbol{\chi}-\mathbf{b}_{p}\right)+\sum_{k \in I}\left\|F_{k}^{I} \mathbf{r}_{I}\left(\mathbf{z}_{I_{k} I_{k+1}}^{I}, \boldsymbol{\chi}\right)\right\|_{\Sigma_{k+1}^{l_{k}}}^{2}+\right. \\ \left.\sum_{k \in O}\left\|F_{k}^{O} \mathbf{r}_{O}\left(\mathbf{z}_{I_{k} I_{k+1}}^{O}, \boldsymbol{\chi}\right)\right\|_{\Sigma_{k+1}^{\alpha_{k}}}^{2}+\sum_{(l, j) \in C} \rho\left(\left\|F_{k}^{C} \mathbf{r}_{C}\left(\mathbf{z}_{l}^{C_{j}}, \boldsymbol{\chi}\right)\right\|_{\Sigma_{l}^{c_{j}}}^{2}\right)\right\} \end{array}\]-
实验结果
因为没有encoder+IMU+camera的公开数据集,作者是用的自己的设备进行实验:
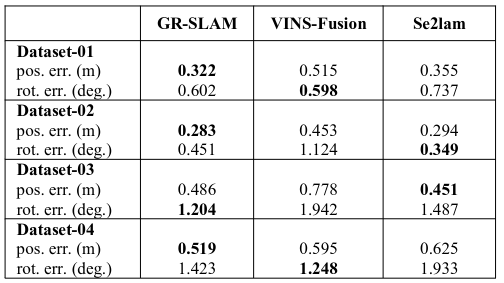
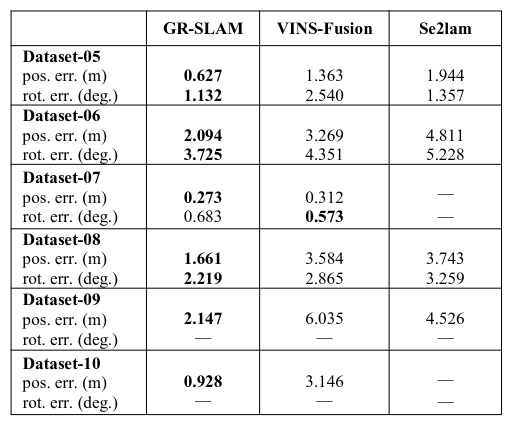
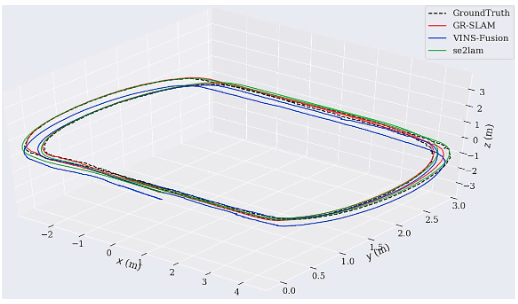
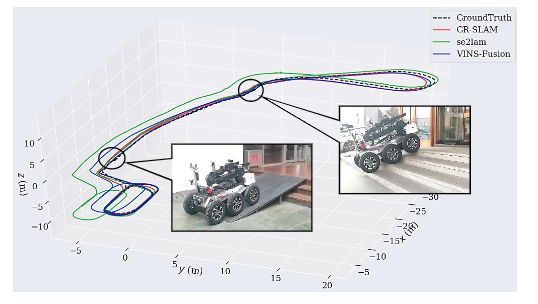
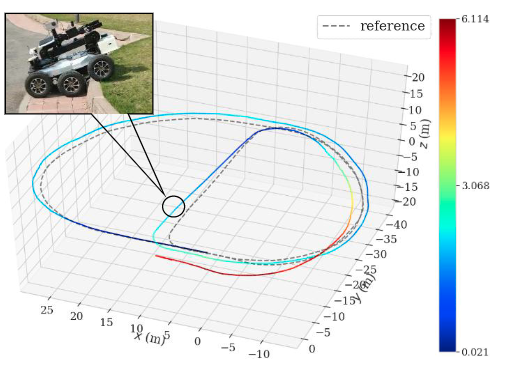
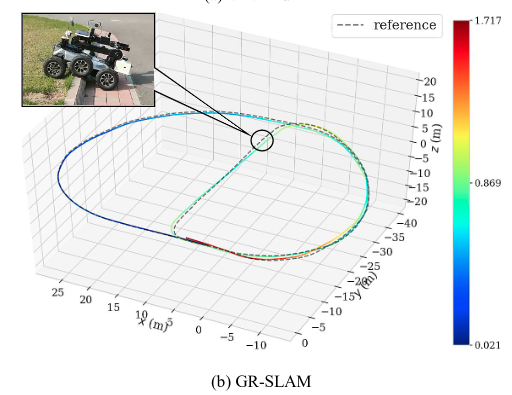
Conclusion
这篇文章,解决的问题是VIO在地面行驶的Z轴不确定性问题,这个问题在实验中也遇到过,不过没有什么比较好的方案,从他的实验效果中来看,z轴约束还是不错的,值得一试,他的动态权重方式也挺有意思,可以考虑移植到自己代码中。
