《PLF-VINS: Real-Time Monocular Visual-Inertial SLAM With Point-Line Fusion and Parallel-Line Fusion》(RAL2021)

Motivation

角点和线特征提供了大量的物体结构信息，在二维图像中，角点和线特征具有位置相似性，所以对于角点特征和线特征的融合是有利于提升定位精度的。

Contribution

1. 我们提出了一种点线耦合（PLC）特性和PLC残来紧密耦合点和线。PLC特征基于位置相似性来提取，这个特征从实验上来看提升了鲁棒性和精确度。
2. 提出了一个三维的并行线残差使得线特征和PLC特征更加鲁棒，引入这个特征的核心在于检测多视图的灭点。
3. 在EUROC数据集上体现了有竞争力的结果。

Content

1. 系统概述

系统框架的基础是基于VINS的，在VINS的基础上跟踪点特征和线特征，角点通过KLT跟踪，线特征使用LSD描述子，LBD来跟踪线

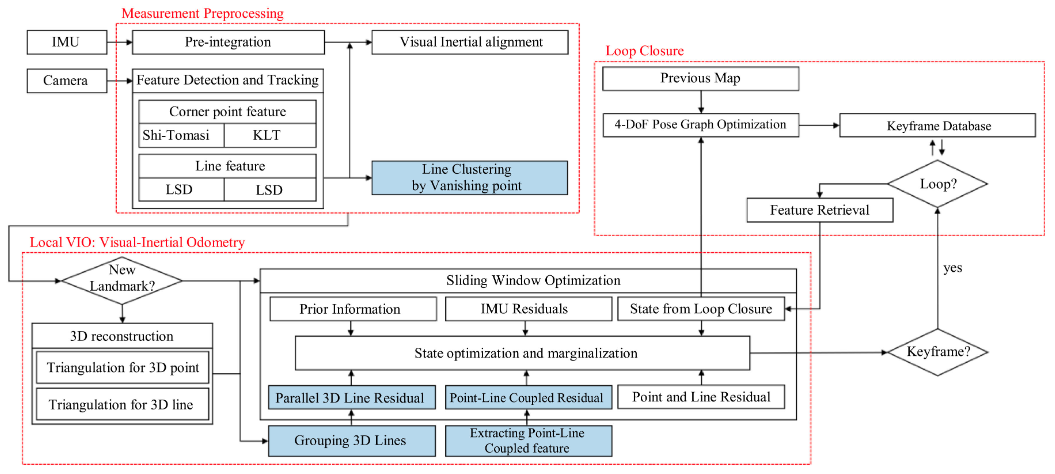
1. 前端滑窗优化

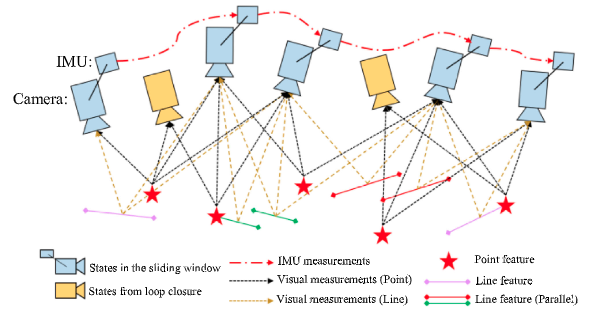
优化公式如下:

基本和vins一样，多出来的部分，主要分为三个，分别是线残差（线到端点），PLC残差，和并行线残差.

\[\begin{array}{l} \min _{x}\left\{\left\|r_{p}-H_{p} X\right\|^{2}+\sum_{k \in \mathcal{B}} r_{\mathcal{B}}\left\|\left(z_{b_{k+1}}^{b_{k}}, \mathcal{X}\right)\right\|_{P_{b_{k+1}}^{b_{k}}}^{2}\right. \\ +\sum_{(l, j) \in \mathcal{C}} \rho\left(\left\|r_{\mathcal{C}}\left(z_{l}^{c_{j}}, \mathcal{X}\right)\right\|_{P_{l}^{c_{j}}}^{2}\right)+\sum_{(\gamma, j) \in \mathcal{L}} \rho\left(\left\|r_{\mathcal{L}}\left(z_{\gamma}^{c_{j}}, x\right)\right\|_{\mathcal{L}_{\mu}^{c_{j}}}^{2}\right) \\ \left.+\sum_{(l, \gamma, j) \in \mathcal{F}} \rho\left(\left\|r_{\mathcal{F}}\left(z_{l}^{c_{j}}, z_{\gamma}^{c_{j}}, \mathcal{H}, \mathcal{X}\right)\right\|^{2}\right)+\sum_{\left(\gamma_{i}, \gamma_{j}\right) \in \mathcal{P}} \rho\left(\left\|r_{\mathcal{P}}(\mathcal{X})\right\|^{2}\right)\right\} \end{array}\]

1. 提取PLC特征

   角点一般出现在曲率变化快的地方，这个地方一般是多个线段的交点，也就是很有可能是直线的端点，所以角点和线特征具有很强的相关性，这个相关性被定义为PLC特征。

   为了将检测出的线特征和角点特征进行分组，首先要基于点特征搜索线的端点(以这个点特征为半径搜索最近距离的线特征)，如果成功搜索到，则生成一个PLC描述子:

\[\mathcal{H}=\left\{h \mid h=\left\{l, \gamma, c_{i}, c_{j}\right\}\right\}\]

搜索过程如下:

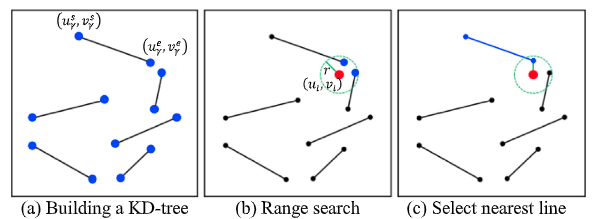
1. 点线融合残差

   基于优化的VIO使用BA估计点的深度，深度估计的精确性和稳定性受到跟踪帧的数量的影响，在这个工作中，作者设定如果点特征的跟踪帧的数量小于阈值，则加入PLC残差:

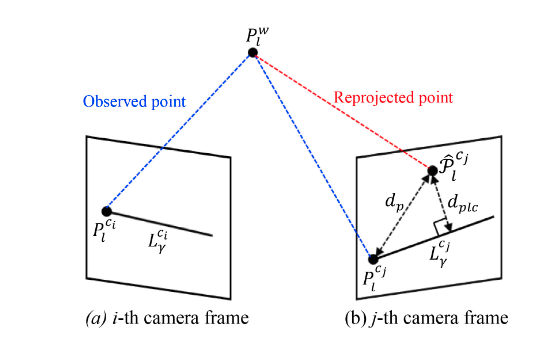
残差计算过程如下:

\[\begin{array}{l} a x+b y+c=0 (直线表达式)\\ \mathcal{M}\left(L_{\gamma}^{c_{j}}\right)=[a, b, c](线性方程的常数系数)\\ a=\left(\frac{y_{\gamma(e)}^{c_{j}}-y_{\gamma(s)}^{c_{j}}}{x_{\gamma(e)}^{c_{j}}-x_{\gamma(s)}^{c_{j}}}\right) b=-1, \mathrm{c}=y_{\gamma(e)}^{c_{j}}-a \cdot x_{\gamma(e)}^{c_{j}} (计算线常系数的过程)\\ \hat{\mathcal{P}}_{l}^{c_{j}}=R_{b}^{c} \\ \left(R_{w}^{b_{j}}\left(R_{b_{i}}^{w}\left(R_{c}^{b} \frac{1}{\lambda}\left[\begin{array}{r} x_{l}^{c_{j}} \\ y_{l}^{c_{j}} \\ 1 \end{array}\right]+\mathrm{p}_{c}^{b}\right)+\mathrm{p}_{b_{i}}^{w}-\mathrm{p}_{b_{j}}^{w}\right)-\mathrm{p}_{c}^{b}\right)(重投影) \\ r_{\mathcal{F}}\left(z_{l}^{\mathrm{c}_{j}}, z_{\gamma}^{\mathrm{c}_{j}}, \mathcal{H}, \mathcal{X}\right)=d_{p l c} \cong \frac{\left(\mathcal{M}\left(L_{\gamma}^{c_{j}}\right) \cdot\left[\hat{\mathcal{P}}_{l}^{c_{j}}\right]^{T}\right)^{2}}{\sqrt{a^{2}+b^{2}}} \end{array}(PLC残差)\]

1. 并行线融合

   采用基于灭点的线聚类方法,基于三维线的平行度增加一个约束。

   对于并行三维线的分类，同时估计三个灭点并执行分类工作(这个工作是基于另一个论文，不作描述)，对于仅仅在一帧内检测到的线族，不作记录，理由如下图:

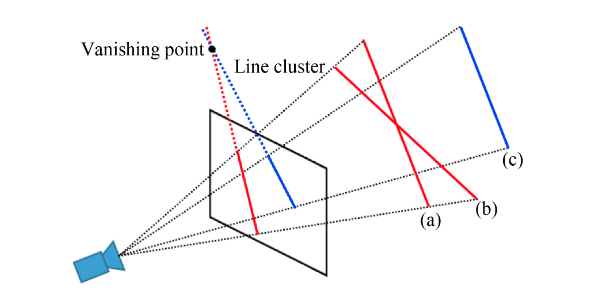
实际执行的效果如下:

对于上述不作记录的线族，通过持续性检测，可以把它们加入到记录:

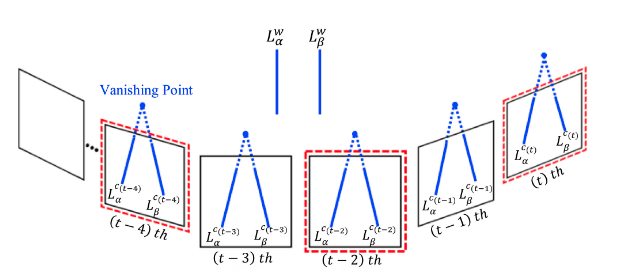
并行线残差的表示形式如下:

\[r_{\mathcal{P}}(\chi)=\left(d_{\alpha}^{T} \cdot n_{\beta}^{T}+n_{\alpha}^{T} \cdot d_{\beta}^{T}\right)^{2}+\left\|d_{\alpha}^{T} \times d_{\beta}^{T}\right\|_{2}^{2}\]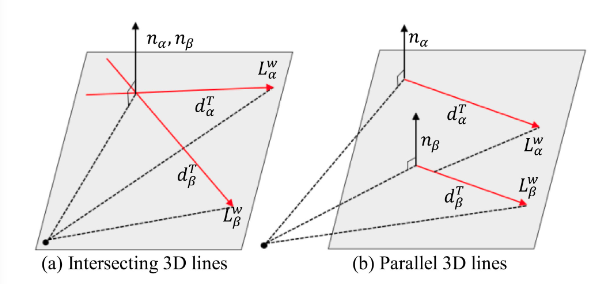

1. 实验结果

   无回环的euroc

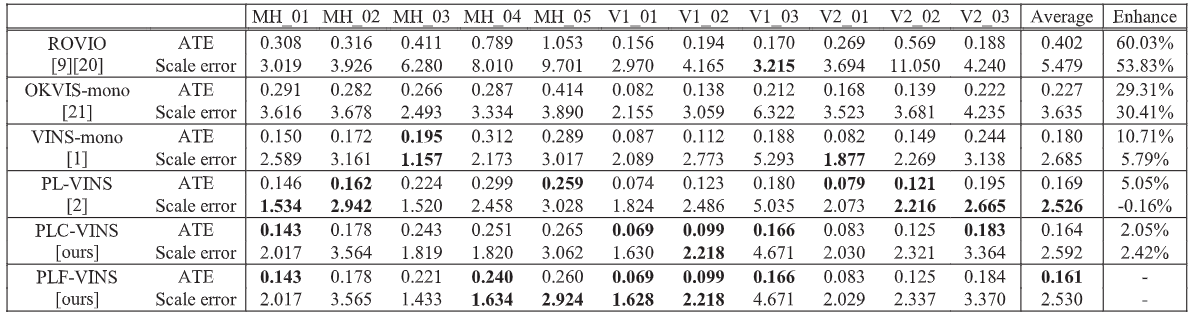
有回环的euroc

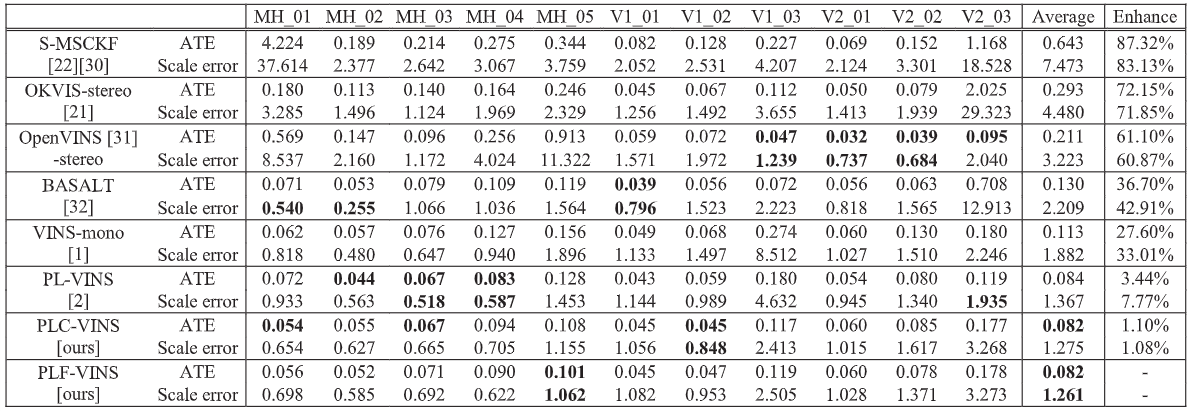
运行时间:

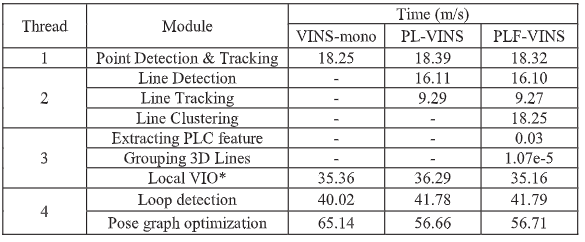
Conclusion

这篇论文在VINS的基础上加入点线融合残差和并行线残差，从实验效果上来看，确实比vinsmono好了点，但是很多场景不如PL-VINS和openvins,不知道是因为什么，可能是并行线残差并不是一个有效的特征?