《π-LSAM: LiDAR Smoothing and Mapping With Planes》(ICRA2021)

Motivation

针对目前广泛使用的loam框架，作者认为有两个问题，一个是不包括BA，另外是位姿精度低(尤其是室内环境)。所以这篇论文的出发点主要是解决loam框架的室内环境缺陷。具体的讲，前端提取面特征作为地标，后段引入面调整来优化位姿。

Contribution

1. 我们引入了平面调整（PA），它联合优化关键帧姿势和平面参数以最小化后端中的点到平面距离。
2. 提出pi参数来降低PA的复杂度
3. 我们提出了一种有效的方法来对准两个平面扫描以检测环路闭合
4. 引入了一个ICP过程，以实现实时全局地图注册。与只考虑两点云之间数据关联的传统ICP不同，我们的ICP过程保持逐扫描的数据关联，这允许我们在激光雷达扫描中直接识别平面，而无需在每次扫描中明确执行耗时的平面检测。
5. 地图表示为平面参数，易于存储和更新。相反，基于ICP的方法（如loam）中的地图为通常组织为KD树, 存储耗时耗空间。

Content

1. 系统框图

   前端建立局部到全局的点到平面的约束, 通过ICP流程实施，并提供实时全局一致姿态。后段联合优化面和关键帧的位姿。

   

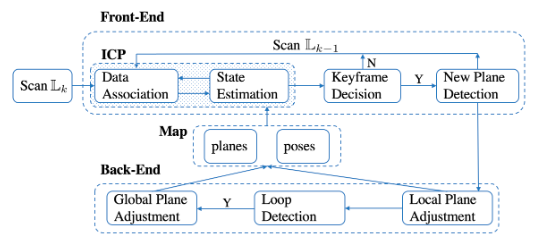
2. 平面特征提取

   使用$\pi$来表示平面:

\[\pi=[n:d]\\ \|n\|_2=1\]

因为$pi$有三个自由度，所以采用最近点向量来参数化:

\[CP(\pi)=dn\]

点搜索前首先将点云组织成range image，然后最近点搜索的范围限制在相邻的两行之间。并且在实际过程中只保存大于50个点的平面。

1. 基于ICP的全局注册

   如下图，首先要进行数据关联，这一步的目的是把两帧观测到的平面点集进行关联，如果关联成功则确定两个平面的关系，如果关联失败则添加新的平面。

   计算位姿采用的是点到面约束:

\[d=\pi^{T}_nT_tp^{k+1}_{ni}\]

跟传统的点到面的约束相比较，主要提升了时间的性能。

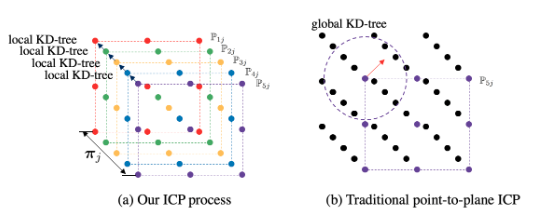
1. 关键帧选择策略

   一是备选平面点云集超过三成的点无法匹配

   二是当前帧和上一个关键帧之间的距离超过了一个阈值

   三是当前帧和上一个关键帧的旋转角度超过了一个阈值

2. PA(平面调整)

   类似于VO的BA（同时优化三维点和相机位姿），这里采用同时优化平面参数和位姿的方法来约束后段，下图是优化的因子图:

   

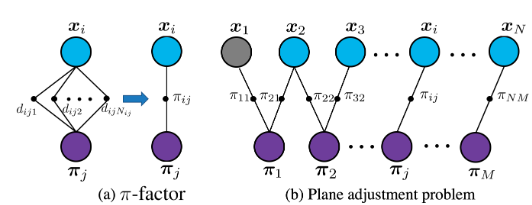
   首先可以将上面的点面误差通过累加的方式得到一个新的PA误差:

\[E=\frac{1}{2}\sum^N_{i=1}\sum^M_{j=1}\sum^{N_{i,j}}_{k=1}d^2_{i,j,k}\]

显而易见的是这个复杂度十分高，因为直接受制于平面点集的点的个数，所以通过引入$\pi$参数的方法来简化。

\[d^2_{ijk}=\pi^T_{j}T_ipp^TT^T\pi\\ =\pi^TTGT^T\pi\\ \pi_{ij}(T_i,\pi_j)=\sqrt{c_{i,j}(T_i,\pi_j)}\]

$pi$参数的形式很方便加入到因子图，对于每个点集只需要计算一次G,这个显著的减少了优化所需要的时间。

最后PA的代价函数形式可以重写如下:

\[E=\frac{1}{2}\sum\sum\pi^2_{ij}(T,\pi)\]

1. LPA(局部平面调整)

   这个是为了进一步提高计算效率，引入了滑窗的思想，在一段滑窗内构建因子图进行优化。

   除了按照时序更新滑窗以外，还按照下面三个准则来剔除关键帧:

   一是这个关键帧不包括一个新的平面，或者它的新的平面全部被剔除

   二是两个关键帧之间的距离小于0.3m，则剔除后面的关键帧。

   三是两个关键帧之间的旋转角度小于15度，则剔除后面的关键帧。

2. GPA(全局平面调整)

   这个部分的目的是执行另一个优化全部平面的线程来辅助优化，执行频率文章中虽然没说，不过应该很低。

3. 实验结果

   

   

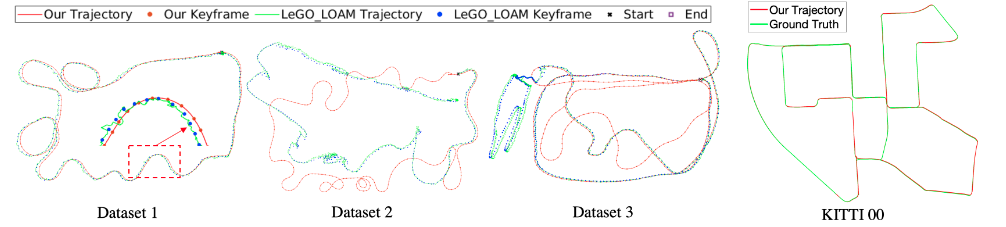
Conclusion

这篇论文，感觉是基于loam的点面残差，再结合另一个作者提出的平面表示方式，从而提出了一个新的形式化的平面残差，后段的贡献比较大，通过建立一个面因子图，实现了类似于视觉BA的PA。