《Colored Point Cloud Registration Revisited》(ICCV2017)

Motivation

作者认为传统的点云配准方法(比如ICP),在面对平滑点云等目标时，结果偏差会很大，为了解决这个问题，作者想要加入色彩信息来进行额外的约束。一个关键的挑战是颜色只能定义在三维空间中的离散点上。为了优化一个连续的联合目标，需要定义一个连续的、可微的光度项，其梯度表示颜色如何随位置变化。基于密集和直接的RGB-D图像对齐公式，使用二维图像平面作为参数化域，为了定义点云对齐的光学目标，在每个点的切面上引入了一个虚拟图像，它提供了隐式颜色变化的局部近似。利用这种结构，将用于RGB-D图像对齐的光度学目标推广到非结构化点云对齐。

Contribution

1. 提供了一种新的彩色点云配准方法
2. 由于点云配准在高保真场景重建中起着核心作用，因此我们使用所提出的算法来增强最先进的场景重建系统。
3. 为了定量评估真实场景的重建精度，我们建立了一个工业激光扫描仪扫描的室内场景数据集。实验表明，增强后的管道可以产生更精确的重建结果。

Content

1. RGB-D图像对齐

   通过下面这个残差函数: \(E(T)=(1-\delta)E_{I}(T)+\delta E_{D}(T)\\ E_D(T)=\sum_{x}(D_i(x^`)-g_d(s(h(x,D_j(x)),T)))^2\\ E_I(T)=\sum_{x}(I_i(x^`)-I_j(x))^2\)

2. 参数化

   将原来点的离散光度连续化: \(C_{p}(u)=C(p)+d_p^Tu\\ \mathbf{f}(\mathbf{s})=\mathbf{s}-\mathbf{n}_{\mathbf{p}}(\mathbf{s}-\mathbf{p})^{\top} \mathbf{n}_{\mathbf{p}}\\ \begin{aligned} L\left(\mathbf{d}_{\mathbf{p}}\right) &=\sum_{\mathbf{p}^{\prime} \in \mathcal{N}_{\mathbf{p}}}\left(C_{\mathbf{p}}\left(\mathbf{f}\left(\mathbf{p}^{\prime}\right)-\mathbf{p}\right)-C\left(\mathbf{p}^{\prime}\right)\right)^{2} \\ & \approx \sum_{\mathbf{p}^{\prime} \in \mathcal{N}_{\mathbf{p}}}\left(C(\mathbf{p})+\mathbf{d}_{\mathbf{p}}^{\top}\left(\mathbf{f}\left(\mathbf{p}^{\prime}\right)-\mathbf{p}\right)-C\left(\mathbf{p}^{\prime}\right)\right)^{2} \end{aligned}\)

3. 优化目标函数

\[E(T)=(1-\delta)E_c(T)+\delta E_G(T)\\\]

将点投影到切平面后，最终的目标函数变成几何误差和光度误差的权重和

\[q^`=f(s(q,T))\\ E_C(T)=\sum(C_p(q^`)-C(q))^2\\ E_G(T)=\sum(G_p(q^`)-(o_p-s(q,T))^Tn_p)^2\\ \begin{aligned} E(\mathbf{T}) &=(1-\sigma) \sum_{(\mathbf{p}, \mathbf{q}) \in \mathcal{K}}\left(r_{C}^{(\mathbf{p}, \mathbf{q})}(\mathbf{T})\right)^{2} \\ &+\sigma \sum_{(\mathbf{p}, \mathbf{q}) \in \mathcal{K}}\left(r_{G}^{(\mathbf{p}, \mathbf{q})}(\mathbf{T})\right)^{2} \end{aligned}\\ \begin{aligned} &r_{C}^{(\mathbf{p}, \mathbf{q})}(\mathbf{T})=C_{\mathbf{p}}(\mathbf{f}(\mathbf{s}(\mathbf{q}, \mathbf{T})))-C(\mathbf{q}) \\ &r_{G}^{(\mathbf{p}, \mathbf{q})}(\mathbf{T})=(\mathbf{s}(\mathbf{q}, \mathbf{T})-\mathbf{p})^{\top} \mathbf{n}_{\mathbf{p}} . \end{aligned}\]

雅克比:

\[\mathbf{T} \approx\left(\begin{array}{cccc} 1 & -\gamma & \beta & a \\ \gamma & 1 & -\alpha & b \\ -\beta & \alpha & 1 & c \\ 0 & 0 & 0 & 1 \end{array}\right) \mathbf{T}^{k}\\ \mathbf{J}_{\mathbf{r}}^{\top} \mathbf{J}_{\mathbf{r}} \xi=-\mathbf{J}_{\mathbf{r}}^{\top} \mathbf{r}\\ \begin{aligned} \mathbf{r} &=\left[\sqrt{1-\sigma} \mathbf{r}_{C} ; \sqrt{\sigma} \mathbf{r}_{G}\right] \\ \mathbf{r}_{C} &=\left[\left.r_{C}^{(\mathbf{p}, \mathbf{q})}(\mathbf{T})\right|_{\mathbf{T}=\mathbf{T}^{k}}\right]_{(\mathbf{p}, \mathbf{q})} \\ \mathbf{r}_{G} &=\left[\left.r_{G}^{(\mathbf{p}, \mathbf{q})}(\mathbf{T})\right|_{\mathbf{T}=\mathbf{T}^{k}}\right]_{(\mathbf{p}, \mathbf{q})} \\ \mathbf{J}_{\mathbf{r}} &=\left[\sqrt{1-\sigma} \mathbf{J}_{\mathbf{r}_{C}} ; \sqrt{\sigma} \mathbf{J}_{\mathbf{r}_{G}}\right] \\ \mathbf{J}_{\mathbf{r}_{C}} &=\left[\left.\nabla r_{C}^{(\mathbf{p}, \mathbf{q})}(\mathbf{T})\right|_{\mathbf{T}=\mathbf{T}^{k}}\right]_{(\mathbf{p}, \mathbf{q})} \\ \mathbf{J}_{\mathbf{r}_{G}} &=\left[\left.\nabla r_{G}^{(\mathbf{p}, \mathbf{q})}(\mathbf{T})\right|_{\mathbf{T}=\mathbf{T}^{k}}\right]_{(\mathbf{p}, \mathbf{q})} . \end{aligned}\]

1. 从粗到细的优化过程

   建立了一个点云金字塔通过减少采样输入点云和使用体素网格和增加体素大小的方法来粗化。下采样算法用它们的中心点来逼近每个体素中的点。因此，就优化目标而言，较粗水平的残差是较细水平的多个残差的组合。在较粗的层次上，目标函数更为光滑，可以指导高斯-牛顿法达到更深的极小值。

1. 实验结果

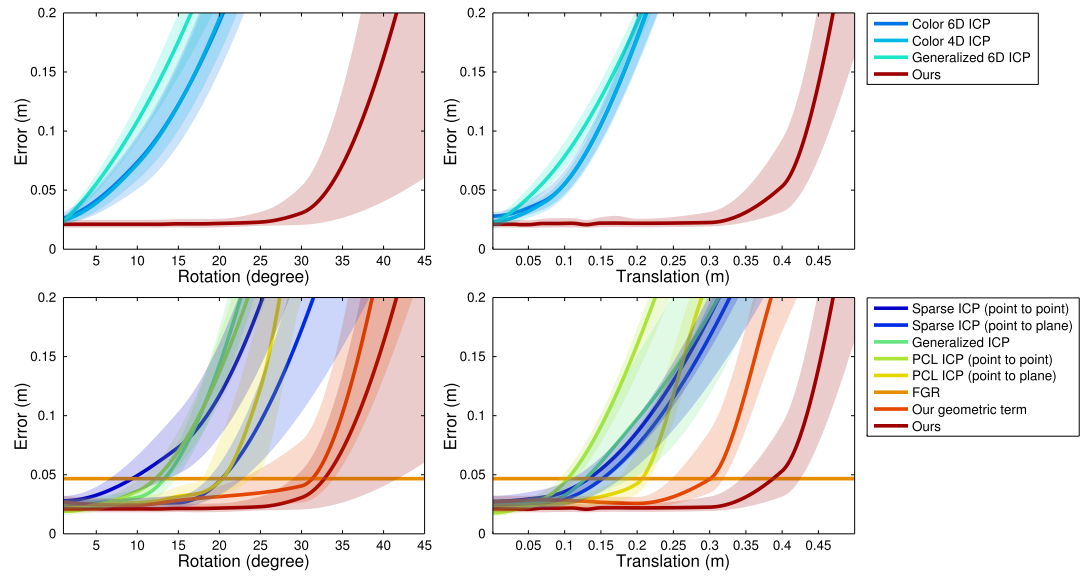
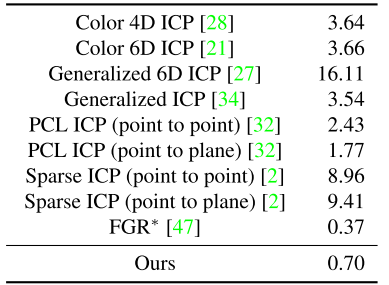
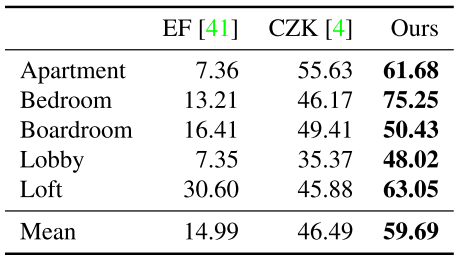
Conclusion

这篇论文比较早，主要是提供了一个彩色点云配准的方案，方法是连续化点云的光度以后，将点云的光度残差和深度残差一起进行优化，从效果来看是不错的，值得借鉴。