这篇博客并不是完全原创,其中部分内容参考:
https://blog.csdn.net/Yong_Qi2015/article/details/116549378
《TEASER:Fast and Certifiable Point Cloud Registration》(TRO2020)
Motivation
求解带有外点的鲁邦估计是比较困难的,只能提供相对容易的检测条件来判断检测的结果是否最优。本文为了解决带有外点的鲁邦估计问题,首先使用TLS(截断最小二乘)将配准问题重新建模,然后通过一个图理论框架将尺度旋转平移三个评价尺标解耦,最后再通过渐进非凸性求解旋转子问题。

Contribution
- 开发了估计尺度的不变测量量。
- 在噪声未知但有界的假设下,将尺度位移旋转解耦形式化。
- 提供了一个通用的图理论框架,用于推导这些不变测量量。
- 展示这个框架通过寻找不变测量量定义的图的最大派系,允许修剪大量的外点。
- 证明了使用adaptive voting机制能够在多项式时间内精确地求解标量例子的TLS估计问题,这就能够高效地进行尺度和分量形式平移的估计
- 证明了能够建立一个紧的半定规划(SDP)松弛去估计旋转,同时建立一个后验条件去检测松弛的质量
- 在无噪声例子中,提供了易于检查的条件,其中TEASER在外点存在的情况下恢复出了点云之间的变换
- 在有噪声例子中,在TEASER估计和真值变换之间的距离上提供了界
- 实现TEASER的一个快速版本,称为TEASER++,使用渐进非凸(GNC)估计旋转而不需要求解大规模SDP
- TEASER++毫秒级运行,是目前最快的鲁棒配准算法
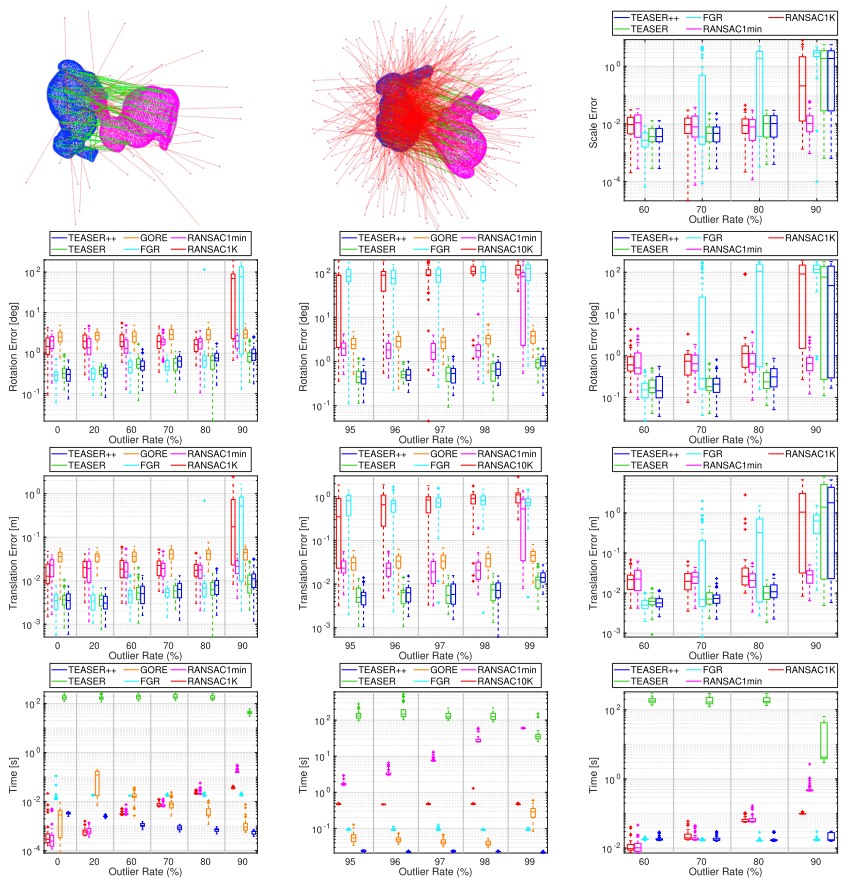
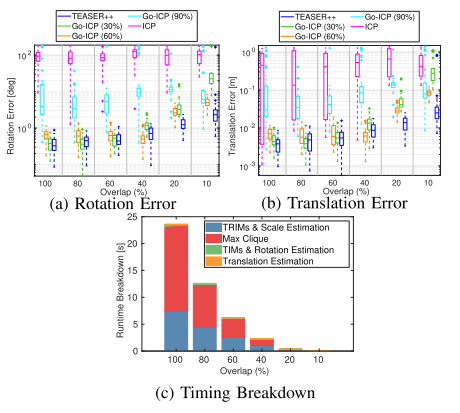
- TEASER++非常鲁棒使得它能够求解对应点未知的问题(如假设所有对所有的对应点情况),并且它显著地超越ICP,比Go-ICP更精确,同时要快几个数量级
- 当和基于深度学习的关键点检测和匹配相结合时,TEASER++能够提升配准性能
- 当尺度已知时它们对于超过99%外点率的情况都是鲁棒的。
Content
原论文内容很多,很多篇幅是展示的证明,下面主要讲一下算法的主要流程:
-
使用截断最小二乘代价函数的鲁棒配准
给定两组点云$a_i,b_i$, 测量噪声是$\delta_i$,原始内参外参向量是$o_i$, 原始问题可以描述成: \(b_i=s^oR^oa_i+t^o+o_i+\delta_i\)
可以表示成非线性最小二乘的形式:
假设噪声未知但是有界,为了对外点不敏感,可以变换成TLS:
\[min\sum^N_{i=1}(\frac{1}{\beta^2_i}\|b_i-sRa_i-t\|^2,\hat{c}^2)\]-
尺度旋转平移解耦
首先进行平移不变测量,通过求取两个点云的相对位置进行相减来抵消平移的影响: \(b_j-b_i=sR(a_j-a_i)+(o_j-o_i)+(\delta_j-\delta_i)\)
然后进行旋转不变测量,这个需要计算出刚刚平移不变测量的范数:
因为噪声有界,所以可以转换成:
\[\|\hat{b_{i,j}}\|=\|sRa_{i,j}\|+o_{i,j}+\delta_{i,j}\]进行归一化表示为:
\[s_{i,j}=\frac{b_{i,j}}{a_{i,j}}=s+o^s_{i,j}+\delta^s_{i,j}\]总结起来,解耦的过程可以描述为下表:

-
TLS
TRIM估计尺度,采用自适应的投票算法: \(\hat{s}=argmin_{s}\sum^K_{k=1}min(\frac{(s-s_k)^2}{\alpha^2_k},\hat{c}^2)\)
TIMS估计旋转,采用SDP半定松弛算法
最后,在已经估计出旋转和尺度的情况下,采用自适应投票算法估计平移:
\[\hat{t}_j=argmin\sum^N_{i=1}min(\frac{(t_j-[b_i-\hat{s}\hat{R}a_i]_j)^2}{\beta^2_i},\hat{c}^2)\]上述的步骤总结伪代码如下

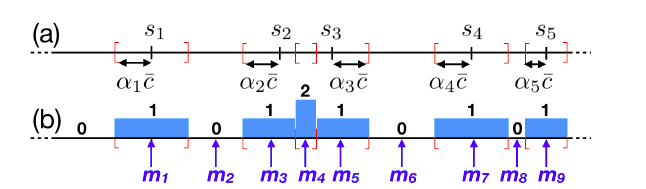
自适应投票算法如下:

第4行的排序和6-12的投票算法如下:
最后一行的公式是计算尺度估计值如下:
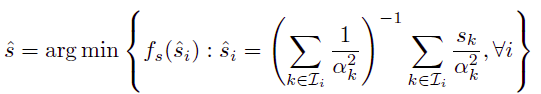
….中间的证明内容不作细表
- 实验